题目内容
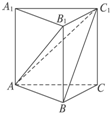
如图,在正三棱柱ABC-A1B1C1中,AB=1.若二面角C-AB-C1的大小为60°,则点C到平面ABC1的距离为______.
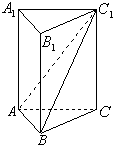

如图,在正三棱柱ABC-A1B1C1中,AB=1.若二面角C-AB-C1的大小为60°,
过C作CD⊥AB,D为垂足,连接C1D,则C1D⊥AB,∠C1DC=60°,CD=
,
则C1D=
,CC1=
,在△CC1D中,过C作CE⊥C1D,
则CE为点C到平面ABC1的距离,CM=
=
,
所以点C到平面ABC1的距离为
.
故答案为:

过C作CD⊥AB,D为垂足,连接C1D,则C1D⊥AB,∠C1DC=60°,CD=
| ||
| 2 |
则C1D=
| 3 |
| 3 |
| 2 |
则CE为点C到平面ABC1的距离,CM=
| ||||||
|
| 3 |
| 4 |
所以点C到平面ABC1的距离为
| 3 |
| 4 |
故答案为:
| 3 |
| 4 |


练习册系列答案
相关题目