题目内容
【题目】已知数列{an},{bn}满足a1=2,b1=4,且 2bn=an+an+1 , an+12=bnbn+1 .
(Ⅰ)求 a 2 , a3 , a4及b2 , b3 , b4;
(Ⅱ)猜想{an},{bn}的通项公式,并证明你的结论;
(Ⅲ)证明:对所有的 n∈N* , ![]()
![]() …
… ![]() <
< ![]() <
< ![]() sin
sin ![]() .
.
【答案】解:(I)令n=1得 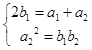 ,解得
,解得 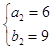 ,
,
令n=2得 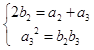 ,解得
,解得 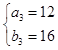 ,
,
令n=3得 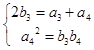 ,解得
,解得 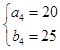 .
.
(II)猜想:an=n(n+1),bn=(n+1)2.
证明:当n=1时,猜想显然成立,
假设n=k(k≥1)猜想成立,即ak=k(k+1),bk=(k+1)2,
∵2bk=ak+ak+1,∴ak+1=2bk﹣ak=2(k+1)2﹣k(k+1)=(k+1)(k+2),
∵ak+12=bkbk+1,∴bk+1= ![]() =(k+2)2,
=(k+2)2,
∴当n=k+1时,猜想成立,
∴an=n(n+1),bn=(n+1)2,n∈N+.
(III)证明:由(II)可知 ![]() =
= ![]() ,
,
于是原不等式等价于 ![]() …
… ![]() <
< ![]() <
< ![]() sin
sin ![]() ,
,
(i)先证 ![]() …
… ![]() <
< ![]() ,
,
∵4n2﹣1<4n2,∴(2n+1)(2n﹣1)<4n2,
∴(2n﹣1)2(2n+1)<4n2(2n﹣1),
即( ![]() )2<
)2< ![]() ,即
,即 ![]() <
< ![]() ,
,
∴ ![]() …
… ![]() <
< ![]()
![]()
![]() …
… ![]() =
= ![]() ,
,
(ii)再证 ![]() <
< ![]() sin
sin ![]() .
.
令 ![]() =x,则0<x≤
=x,则0<x≤ ![]() <
< ![]() ,
,
设f(x)=x﹣ ![]() sinx,则f′(x)=1﹣
sinx,则f′(x)=1﹣ ![]() cosx<0,
cosx<0,
∴f(x)在(0, ![]() )上单调递减,
)上单调递减,
∴f(x)<f(0)=0,即x ![]() sinx,
sinx,
∴ ![]() <
< ![]() sin
sin ![]() .
.
综上,对所有的 n∈N*, ![]()
![]() …
… ![]() <
< 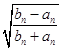 <
< ![]() sin
sin 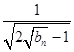
【解析】(I)依次把n=1,2,3代入递推式即可求出{an},{bn}的前4项;(II)利用数学归纳法证明猜想;(III)利用放缩法证明不等式左边,利用函数单调性证明不等式右边.
【考点精析】解答此题的关键在于理解归纳推理的相关知识,掌握根据一类事物的部分对象具有某种性质,退出这类事物的所有对象都具有这种性质的推理,叫做归纳推理.

 习题精选系列答案
习题精选系列答案