题目内容
【题目】已知函数f（x）= 
+alnx﹣2，曲线y=f（x）在点P（1，f（1））处的切线与直线y=x+3垂直．
（1）求实数a的值；
（2）记g（x）=f（x）+x﹣b（b∈R），若函数g（x）在区间[e﹣1 ， e]上有两个零点，求实数b的取值范围；
（3）若不等式πf（x）＞（ 
）1+x﹣lnx在|t|≤2时恒成立，求实数x的取值范围．
【答案】
（1）解：函 数 f（ x） 的 定 义 域 为 （ 0，+∞），f′（ x）= 
．
∵曲线y=f（x）在点P（1，f（1））处的切线与直线y=x+3垂直，
∴f′（ 1）=﹣2+a=﹣1，解 得 a=1．
（2）解：g（ x）= 
+lnx+x﹣2﹣b（ x＞0），g′（ x）= 
，
由 g′（ x）＞0，得 x＞1，由 g′（ x）＜0，得 0＜x＜1，
∴g（ x） 的 单 调 递 增 区 间 是 （ 1，+∞），单 调 递 减 区 间 为 （ 0，1），
当 x=1 时，g（ x） 取 得 极 小 值 g（ 1），
∵函 数 g（ x） 在 区 间[e﹣1，e]上 有 两 个 零 点，∴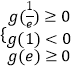 
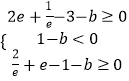，解得1 
，
∴b 的 取 值 范 围 是 （ 1， 
+e﹣1]；
（3）解：∵π f（x）＞（ 
）t+x﹣lnx 在|t|≤2 时 恒 成 立，∴f（ x）＞﹣t﹣x+lnx，
即xt+x2﹣2x+2＞0 在|t|≤2 时 恒 成 立，令 g（ t）=xt+x2﹣2x+2，（x＞0），
∴只 需 g（﹣2）＞0，即 x2﹣4x+2＞0
解 得x∈（ 0，2﹣ 
）∪（2+ ，+∞）
【解析】（1）根据导数的几何意义，得 f′（ 1）=﹣1，解得a，（2）g（ x）= +lnx+x﹣2﹣b（ x＞0），g′（ x）= ，可得当 x=1 时，g（ x） 取 得 极 小 值 g（ 1）；可得函 数 g（ x） 在 区 间[e﹣1，e]上 有 两 个 零 点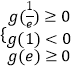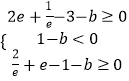， ，解得实数b的取值范围； （3）π f（x）＞（ ）t+x﹣lnx 在|t|≤2 时 恒 成 立，f（ x）＞﹣t﹣x+lnx，即t+x2﹣2x+2＞0 在|t|≤2 时 恒 成 立，令 g（ t）=xt+x2﹣2x+2，x＞0，只 需 g（﹣2）＞0，即可
【考点精析】通过灵活运用函数的最大(小)值与导数，掌握求函数
在
上的最大值与最小值的步骤：（1）求函数在
内的极值；（2）将函数的各极值与端点处的函数值
，
比较，其中最大的是一个最大值，最小的是最小值即可以解答此题．
