Question

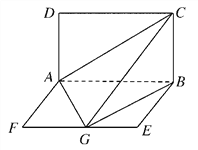
【题目】如图，在四棱锥P ABCD中，AB∥CD，AB⊥AD，CD＝2AB，平面PAD⊥底面ABCD，PA⊥AD，E和F分别为CD和PC的中点．

求证：(1) BE∥平面PAD；

(2) 平面BEF⊥平面PCD.

Answer 1

【答案】（1）见解析；（2）见解析.

【解析】试题分析：(1) 平面平面且,由面面垂直的性质定理可得底面.(2) 可证为平行四边形,得∥,根据线面平行的判定定理证得∥平面.(3)由面面垂直的性质定理可得平面或证, 根据线面垂直的判定定理证平面可得即,依题意可得为矩形,可得,根据线面垂直的判定定理可得平面,从而可得平面⊥平面.

试题解析：证明 (1)平面平面.

又平面平面，且.∴底面. 4分

(2)∵∥， ， 为的中点，

∴∥，且.∴为平行四边形．∴∥.

又∵BE平面PAD，AD平面PAD，∴∥平面. 8分

(3)∵，且四边形为平行四边形．

∴， .

由(1)知底面，则，

∴平面，从而，

又分别为的中点，

∴∥，故.

由， 在平面内，且，∴平面

∴平面⊥平面. 12分