题目内容
已知以向量v= 为方向向量的直线l过点
为方向向量的直线l过点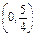 ,抛物线C:y2=2px(p>0)的顶点关于直线l的对称点在该抛物线的准线上.
,抛物线C:y2=2px(p>0)的顶点关于直线l的对称点在该抛物线的准线上.
(1)求抛物线C的方程;
(2)设A、B是抛物线C上两个动点,过A作平行于x轴的直线m,直线OB与直线m交于点N,若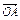 ·
·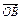 +p2="0" (O为原点,A、B异于原点),试求点N的轨迹方程.
+p2="0" (O为原点,A、B异于原点),试求点N的轨迹方程.
 为方向向量的直线l过点
为方向向量的直线l过点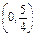 ,抛物线C:y2=2px(p>0)的顶点关于直线l的对称点在该抛物线的准线上.
,抛物线C:y2=2px(p>0)的顶点关于直线l的对称点在该抛物线的准线上.(1)求抛物线C的方程;
(2)设A、B是抛物线C上两个动点,过A作平行于x轴的直线m,直线OB与直线m交于点N,若
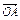 ·
·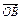 +p2="0" (O为原点,A、B异于原点),试求点N的轨迹方程.
+p2="0" (O为原点,A、B异于原点),试求点N的轨迹方程.(1)y2=4x(2)点N的轨迹方程为x=-2(y≠0)
(1)由题意可得直线l的方程为y=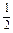 x+
x+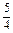 , ①
, ①
过原点垂直于l的直线方程为y="-2x. " ②
解①②得x=-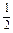 .
.
∵抛物线的顶点关于直线l的对称点在该抛物线的准线上,
∴-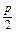 =-
=-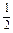 ×2, p=2.
×2, p=2.
∴抛物线C的方程为y2=4x.
(2)设A(x1,y1),B(x2,y2),N(x,y),由题意知y=y1.
由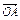 ·
·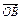 + p 2=0,得x1x2+y1y2+4=0,
+ p 2=0,得x1x2+y1y2+4=0,
又y12=4x1,y22=4x2,解得y1y2="-8, " ③
直线ON:y=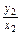 x,即y=
x,即y=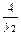 x. ④
x. ④
由③、④及y=y1得点N的轨迹方程为x=-2(y≠0).
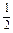 x+
x+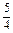 , ①
, ①过原点垂直于l的直线方程为y="-2x. " ②
解①②得x=-
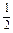 .
.∵抛物线的顶点关于直线l的对称点在该抛物线的准线上,
∴-
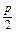 =-
=-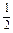 ×2, p=2.
×2, p=2.∴抛物线C的方程为y2=4x.
(2)设A(x1,y1),B(x2,y2),N(x,y),由题意知y=y1.
由
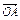 ·
·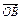 + p 2=0,得x1x2+y1y2+4=0,
+ p 2=0,得x1x2+y1y2+4=0,又y12=4x1,y22=4x2,解得y1y2="-8, " ③
直线ON:y=
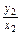 x,即y=
x,即y=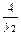 x. ④
x. ④ 由③、④及y=y1得点N的轨迹方程为x=-2(y≠0).

练习册系列答案
相关题目
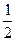 ,1)
,1)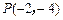 的抛物线的标准方程.
的抛物线的标准方程.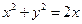 及抛物线S:
及抛物线S: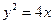 ,过圆心
,过圆心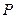 作直线
作直线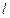 ,此直线与上述两曲线的四个交点,自上而下顺次记为
,此直线与上述两曲线的四个交点,自上而下顺次记为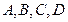 ,如果线段
,如果线段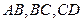 的长按此顺序构成一个等差数列,求直线l的方程.
的长按此顺序构成一个等差数列,求直线l的方程.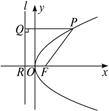
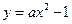 上总存在关于直线
上总存在关于直线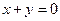 对称的两点,求
对称的两点,求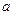 的范围.
的范围.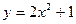 上运动,则P点与点A(0,-1)所连线段中点M的轨迹方程是
上运动,则P点与点A(0,-1)所连线段中点M的轨迹方程是