题目内容
若抛物线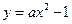 上总存在关于直线
上总存在关于直线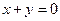 对称的两点,求
对称的两点,求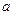 的范围.
的范围.
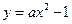 上总存在关于直线
上总存在关于直线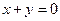 对称的两点,求
对称的两点,求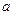 的范围.
的范围.解法一:(对称曲线相交法)
曲线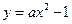 关于直线
关于直线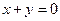 对称的曲线方程为
对称的曲线方程为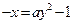 .
.
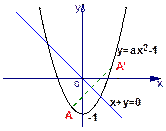
如果抛物线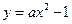 上总存在关于直线
上总存在关于直线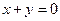 对称的两点,则两曲线
对称的两点,则两曲线
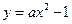 与
与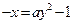 必有不在直线
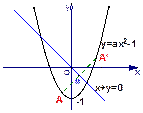
必有不在直线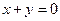 上的两个不同的交点(如图所示),从而可由:
上的两个不同的交点(如图所示),从而可由:
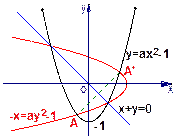
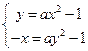
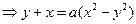
∵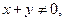
∴
代入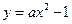 得
得 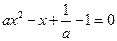 有两个不同的解,
有两个不同的解,
∴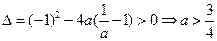 .
.
解法二: (对称点法)
设抛物线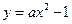 上存在异于于直线
上存在异于于直线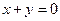 的交点的点
的交点的点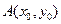 ,且
,且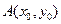 关于直线
关于直线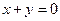 的对称点
的对称点 也在抛物线
也在抛物线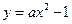 上
上
则
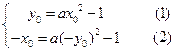 必有两组解
必有两组解
(1)-(2)得
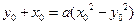 必有两个不同解
必有两个不同解
∵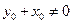 ,
,
∴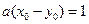 有解
有解
从而有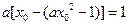 有两个不等的实数解
有两个不等的实数解
即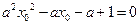 有两个不等的实数解
有两个不等的实数解
∴

∵ ,
,
∴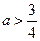

解法三:(点差法)
设抛物线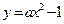 上以
上以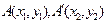 为端点的弦关于直线
为端点的弦关于直线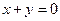 对称,且以
对称,且以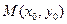 为中点是抛物线
为中点是抛物线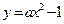 (即
(即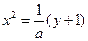 )内的点.
)内的点.
从而有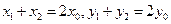 .
.
由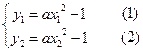
(1)-(2)得
∴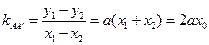
由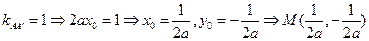

从而有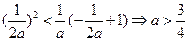 .
.

曲线
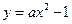 关于直线
关于直线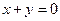 对称的曲线方程为
对称的曲线方程为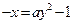 .
.如果抛物线
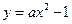 上总存在关于直线
上总存在关于直线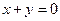 对称的两点,则两曲线
对称的两点,则两曲线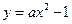 与
与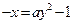 必有不在直线
必有不在直线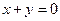 上的两个不同的交点(如图所示),从而可由:
上的两个不同的交点(如图所示),从而可由: 
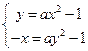
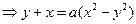
∵
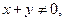
∴

代入
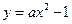 得
得 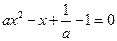 有两个不同的解,
有两个不同的解,∴
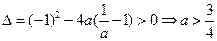 .
. 解法二: (对称点法)

设抛物线
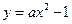 上存在异于于直线
上存在异于于直线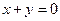 的交点的点
的交点的点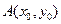 ,且
,且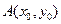 关于直线
关于直线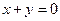 的对称点
的对称点 也在抛物线
也在抛物线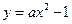 上
上
则
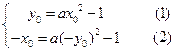 必有两组解
必有两组解
(1)-(2)得
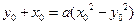 必有两个不同解
必有两个不同解
∵
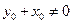 ,
,∴
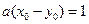 有解
有解
从而有
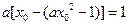 有两个不等的实数解
有两个不等的实数解
即
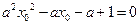 有两个不等的实数解
有两个不等的实数解
∴


∵
 ,
,∴
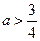

解法三:(点差法)
设抛物线
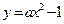 上以
上以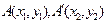 为端点的弦关于直线
为端点的弦关于直线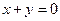 对称,且以
对称,且以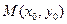 为中点是抛物线
为中点是抛物线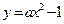 (即
(即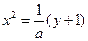 )内的点.
)内的点. 从而有
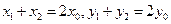 .
. 由
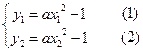
(1)-(2)得

∴
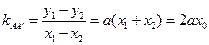
由
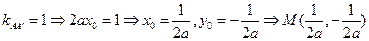

从而有
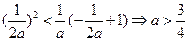 .
.
练习册系列答案
相关题目
 为方向向量的直线l过点
为方向向量的直线l过点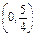 ,抛物线C:y2=2px(p>0)的顶点关于直线l的对称点在该抛物线的准线上.
,抛物线C:y2=2px(p>0)的顶点关于直线l的对称点在该抛物线的准线上.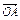 ·
·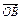 +p2="0" (O为原点,A、B异于原点),试求点N的轨迹方程.
+p2="0" (O为原点,A、B异于原点),试求点N的轨迹方程.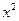 上的一点M到焦点的距离为1,则点M的纵坐标是( )
上的一点M到焦点的距离为1,则点M的纵坐标是( )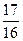
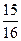
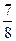
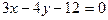
 是抛物线
是抛物线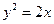 上一动点,点
上一动点,点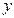 轴上的投影是
轴上的投影是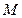 ,点
,点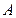 的坐标是
的坐标是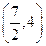 ,则
,则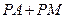 的最小值是( )
的最小值是( )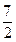
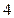
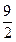
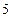
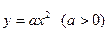 的焦点F作一直线交抛物线于P、Q两点,若PF与FQ的长分别为p、q,则
的焦点F作一直线交抛物线于P、Q两点,若PF与FQ的长分别为p、q,则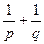 等于 ( )
等于 ( )