题目内容
12.已知函数f(x)=$\left\{{\begin{array}{l}{{3^{-x}}-1,x≥0}\\{1-{3^x},x<0}\end{array}}$,则该函数是( )| A. | 偶函数,且单调递增 | B. | 偶函数,且单调递减 | ||
| C. | 奇函数,且单调递增 | D. | 奇函数,且单调递减 |
分析 由已知中函数的解析式,分析出函数的奇偶性和单调性,进而可得答案.
解答 解:∵函数f(x)=$\left\{{\begin{array}{l}{{3^{-x}}-1,x≥0}\\{1-{3^x},x<0}\end{array}}$,
当x>0时,f(x)=3-x-1,f(-x)=1-3-x,
满足f(-x)=-f(x),且为减函数;
当x=0时,f(0)=0,
满足f(-x)=-f(x),
当x<0时,f(x)=1-3x,f(-x)=3x-1,
满足f(-x)=-f(x),且为增函数;
综上f(x)满足f(-x)=-f(x),且为减函数;
故f(x)为奇函数,且为减函数;
故选:D
点评 本题考查的知识点是分段函数的应用,函数的单调性和奇偶性,分段函数分段讨论是解答的关键.

练习册系列答案
相关题目
20.经过坐标原点,且与圆(x-3)2+(y+1)2=2相切于第四象限的直线方程是( )
| A. | x-y=0 | B. | x+y=0 | C. | x-7y=0 | D. | x+7y=0 |
1.设z1、z2∈C,则“z1、z2均为实数”是“z1-z2是实数”的( )
| A. | 充分非必要条件 | B. | 必要非充分条件 | ||
| C. | 充要条件 | D. | 既非充分又非必要条件 |
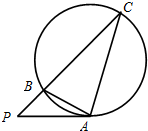 如图,过圆外一点P作圆的切线PA(A为切点),再作割线PBC依次交圆于B,C.若PA=6,PB=3,AB=4,则AC=8.
如图,过圆外一点P作圆的切线PA(A为切点),再作割线PBC依次交圆于B,C.若PA=6,PB=3,AB=4,则AC=8.