题目内容
17.解方程:x4-4x3+x2+4x+1=0.分析 因式分解可得x4-4x3+x2+4x+1=(x2-x-1)(x2-3x-1),从而解得.
解答 解:∵x4-4x3+x2+4x+1=0,
∴(x2-x-1)(x2-3x-1)=0,
∴x2-x-1=0或x2-3x-1=0;
由x2-x-1=0解得,
x1=$\frac{1+\sqrt{5}}{2}$,x2=$\frac{1-\sqrt{5}}{2}$;
由x2-3x-1=0解得,
x3=$\frac{3+\sqrt{13}}{2}$,x4=$\frac{3-\sqrt{13}}{2}$;
故方程x4-4x3+x2+4x+1=0的解为
x1=$\frac{1+\sqrt{5}}{2}$,x2=$\frac{1-\sqrt{5}}{2}$,x3=$\frac{3+\sqrt{13}}{2}$,x4=$\frac{3-\sqrt{13}}{2}$.
点评 本题考查了高次方程的解法,注意因式分解的应用,属于难题.

练习册系列答案
相关题目
12.已知函数f(x)=$\left\{{\begin{array}{l}{{3^{-x}}-1,x≥0}\\{1-{3^x},x<0}\end{array}}$,则该函数是( )
| A. | 偶函数,且单调递增 | B. | 偶函数,且单调递减 | ||
| C. | 奇函数,且单调递增 | D. | 奇函数,且单调递减 |
17.函数f(x)=2x+x-4的零点坐在的区间为( )
| A. | (-1,0) | B. | (0,1) | C. | (1,2) | D. | (2,3) |
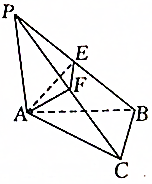 如图所示,已知在△ABC中,∠C=90°,PA⊥平面ABC,AE⊥PB交PB于E,AF⊥PC于F,AP=AB=2,∠AEF=θ,当θ变化时,求三棱锥P-AEF的体积的最大值.
如图所示,已知在△ABC中,∠C=90°,PA⊥平面ABC,AE⊥PB交PB于E,AF⊥PC于F,AP=AB=2,∠AEF=θ,当θ变化时,求三棱锥P-AEF的体积的最大值.