题目内容
8.已知直角坐标系中,直线的参数方程:$\left\{{\begin{array}{l}{x=\sqrt{2}t-\sqrt{2}}\\{y=\sqrt{2}t}\end{array}}\right.$(为参数),以直角坐标系的原点O为极点,轴的非负半轴为极轴建立极坐标系,则以极点为圆心与直线相切的圆的极坐标方程为ρ=1.分析 直线l的参数方程:$\left\{{\begin{array}{l}{x=\sqrt{2}t-\sqrt{2}}\\{y=\sqrt{2}t}\end{array}}\right.$(t为参数),消去参数t可得x=y-$\sqrt{2}$.利用点到直线的距离公式可得:原点到直线的距离r=$\frac{\sqrt{2}}{\sqrt{2}}$=1.即可得出圆的方程.
解答 解:直线l的参数方程:$\left\{{\begin{array}{l}{x=\sqrt{2}t-\sqrt{2}}\\{y=\sqrt{2}t}\end{array}}\right.$(t为参数),消去参数t可得x=y-$\sqrt{2}$.
∴原点到直线的距离r=$\frac{\sqrt{2}}{\sqrt{2}}$=1.
∴以极点为圆心与直线l相切的圆的极坐标方程为ρ=1.
故答案为:ρ=1.
点评 本题考查了把直线的参数方程化为普通方程、直角坐标方程化为极坐标方程、点到直线的距离公式,考查了推理能力与计算能力,属于基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
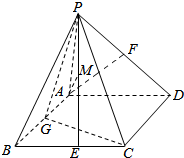 已知在四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD为菱形,∠ABC=60°,AB=PA=2,G、E、F分别为AB、BC、PD的中点
已知在四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD为菱形,∠ABC=60°,AB=PA=2,G、E、F分别为AB、BC、PD的中点 如图,四棱锥P-ABCD中,底面ABCD为菱形,∠BAD=60°,E为CD中点,在PC上找一点F,使得PA∥平面BEF.
如图,四棱锥P-ABCD中,底面ABCD为菱形,∠BAD=60°,E为CD中点,在PC上找一点F,使得PA∥平面BEF.