题目内容
13.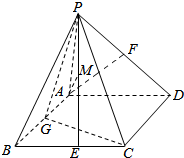 已知在四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD为菱形,∠ABC=60°,AB=PA=2,G、E、F分别为AB、BC、PD的中点
已知在四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD为菱形,∠ABC=60°,AB=PA=2,G、E、F分别为AB、BC、PD的中点(Ⅰ)求证:AF∥平面PGC;
(Ⅱ)若过点A作AM⊥PE,M为垂足,求证:AM⊥PC.
分析 (Ⅰ)取PC的中点H,证明四边形AGHF是四边形即可证明AF∥平面PGC;
(Ⅱ)先证明BC⊥平面PAE,然后证明AM⊥面PBC即可.
解答 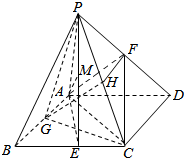 证明:(Ⅰ)取PC的中点H,
证明:(Ⅰ)取PC的中点H,
则HF是△PCD的中位线,
则HF∥CD,且HF=$\frac{1}{2}$CD,
∵G是AB的中点,
∴AG=$\frac{1}{2}$AB=$\frac{1}{2}$CD=HF,AG∥CD∥FH,
则四边形AGHF是四边形,
∴AF∥GH,
∵AF?平面PGC;
GH?平面PGC;
∴AF∥平面PGC;
(Ⅱ)∵E为BC的中点,底面ABCD为菱形,
∴BC⊥AE,
∵PA⊥平面ABCD,
∴PA⊥BC,
∴BC⊥平面PAE,
∵AM?平面PAE
∴BC⊥AM,
∵AM⊥PE,
∴AM⊥面PBC,
∴AM⊥PC.
点评 本题主要考查线面平行和线面垂直的判断,要求熟练掌握相应的判定定理和性质定理.

练习册系列答案
 导学与测试系列答案
导学与测试系列答案 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案
相关题目
4.若x,y是非负整数,那么满足方程25+y2=x2的解有( )
| A. | 1组 | B. | 2组 | C. | 3组 | D. | 4组 |
5.在三棱锥A-BCD中,AC=BD=3,AD=BC=4,AB=CD=m,则m的取值范围是( )
| A. | (1,5) | B. | (1,7) | C. | ($\sqrt{7}$,7) | D. | ($\sqrt{7}$,5) |
2.如果y是x的函数,x=$\sqrt{t+1}$,y=$\sqrt{t-1}$,其中t>1,则y与x的函数表达式为( )
| A. | y=$\sqrt{{x}^{2}-2}$ (x>2) | B. | y=$\sqrt{x-2}$(x>2) | C. | y=$\sqrt{{x}^{2}-2}$ (x>$\sqrt{2}$) | D. | y=$\sqrt{x-2}$(x>$\sqrt{2}$) |
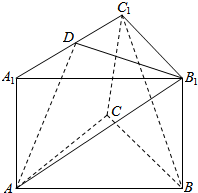 如图,三棱柱ABC-A1B1C1的底面是边长为a的正三角形,侧棱长为$\frac{\sqrt{2}}{2}$a,点D在棱A1C1上.
如图,三棱柱ABC-A1B1C1的底面是边长为a的正三角形,侧棱长为$\frac{\sqrt{2}}{2}$a,点D在棱A1C1上.