题目内容
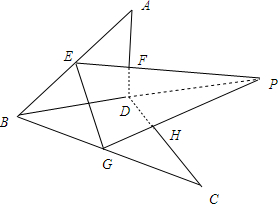
20. 如图,四棱锥P-ABCD中,底面ABCD为菱形,∠BAD=60°,E为CD中点,在PC上找一点F,使得PA∥平面BEF.
如图,四棱锥P-ABCD中,底面ABCD为菱形,∠BAD=60°,E为CD中点,在PC上找一点F,使得PA∥平面BEF.
分析 可连接AC,设交BE于O,从而根据相似三角形的比例关系得出$\frac{CO}{OA}=\frac{1}{2}$,然后可在PC上找到点F,使得$\frac{CF}{FP}=\frac{1}{2}$,这样可连接OF,从而OF∥PA,从而根据线面平行的判定定理得出PA∥平面BEF,这样F点就找到了.
解答  解:如图,连接AC,交BE于O,则△EOC∽△BOA;
解:如图,连接AC,交BE于O,则△EOC∽△BOA;
∴$\frac{CO}{OA}=\frac{CE}{AB}=\frac{1}{2}$;
∴在PC上取F点,使$\frac{CF}{FA}=\frac{1}{2}$,连接OF,则OF∥PA;
又OF?平面BEF,PA?平面BEF;
∴PA∥平面BEF;
这样就在PC上找到了点F,使得PA∥BEF.
点评 考查相似三角形的比例关系,平行线分线段成比例定理,线面平行的判定定理,本题的思路就是,在平面BEF内,找一条过F点平行于PA的直线.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
5.在三棱锥A-BCD中,AC=BD=3,AD=BC=4,AB=CD=m,则m的取值范围是( )
| A. | (1,5) | B. | (1,7) | C. | ($\sqrt{7}$,7) | D. | ($\sqrt{7}$,5) |