题目内容
15.设函数f(x)=$\frac{1}{x}$+ax+b,a,b∈R.(1)若函数y=f(x)-2为奇函数,且函数f(x)在(0,1]上单调递减,在[1,+∞)上单调递增,求函数f(x)的解析式;
(2)当a=1时,方程f(x)=$\frac{1}{2}$x在区间($\frac{1}{2}$,2]有两个不同的实数根,求实数b的最小值;
(3)若对任意的实数b,都存在实数x0∈[$\frac{1}{2}$,2],使得不等式|f(x0)|≥$\frac{1}{2}$成立,求实数a的取值范围.
分析 (1)利用函数g(x)=f(x)-2为奇函数得到b,利用其单调性得到求出a值;
(2)把a=1代入f(x)=$\frac{1}{x}$+ax+b,方程f(x)=$\frac{1}{2}$x化简得x2+2bx+2=0,则在区间[$\frac{1}{2}$,2]有两个不同的实数根,利用根与系数的关系得到关于b的不等式组解之.
(3)由f(x)=$\frac{1}{x}$+ax+b,得$f′(x)=-\frac{1}{{x}^{2}}+a$=$\frac{a{x}^{2}-1}{{x}^{2}}$,判断函数f(x)的单调性,由题意,讨论得到a的范围
解答 解:(1)由题意得,函数y=f(x)-2=$\frac{1}{x}$+ax+b-2,
令g(x)=f(x)-2为奇函数,∴g(-x)=-g(x),
即-$\frac{1}{x}$-ax+b-2=-($\frac{1}{x}$+ax+b-2),解得b=2,
由f(x)=$\frac{1}{x}$+ax+2得,f′(x)=$-\frac{1}{{x}^{2}}+a$,
∵函数f(x)在(0,1]上单调递减,在[1,+∞)上单调递增,
∴f′(1)=-1+a=0,解得a=1,
∴f(x)=$\frac{1}{x}$+x+2;
(2)把a=1代入f(x)=$\frac{1}{x}$+ax+b得,f(x)=$\frac{1}{x}$+x+b,
则方程f(x)=$\frac{1}{2}$x为:$\frac{1}{x}$+x+b=$\frac{1}{2}$x,化简得x2+2bx+2=0,
∵方程f(x)=$\frac{1}{2}$x在区间[$\frac{1}{2}$,2]有两个不同的实数根,
∴x2+2bx+2=0在区间[$\frac{1}{2}$,2]有两个不同的实数根,
则$\left\{\begin{array}{l}{△=4{b}^{2}-8>0}\\{\frac{1}{2}<-b<2}\\{(\frac{1}{2})^{2}+2b×\frac{1}{2}+2>0}\\{{2}^{2}+2b×2+2≥0}\end{array}\right.$,解得$-\frac{3}{2}≤b<-\sqrt{2}$,
∴实数b的最小值是$-\frac{3}{2}$;
(3)由f(x)=$\frac{1}{x}$+ax+b,得$f′(x)=-\frac{1}{{x}^{2}}+a$=$\frac{a{x}^{2}-1}{{x}^{2}}$,
由f′(x)≤0,得a≤$\frac{1}{{x}^{2}}$,所以a≤$\frac{1}{4}$,此时f(x)在区间[$\frac{1}{2}$,2]上为减函数,
要使对任意的实数b,都存在实数x0∈[$\frac{1}{2}$,2],使得不等式|f(x0)|≥$\frac{1}{2}$成立,只要f(x0)≥$\frac{1}{2}$或者f(x0)≤-$\frac{1}{2}$
所以只要f(x)的最大值为f($\frac{1}{2}$)=2+$\frac{1}{2}$a+b$≥\frac{1}{2}$或者f(2)=$\frac{1}{2}$+2a+b$≤-\frac{1}{2}$.
解得a$≤\frac{1}{3}$.,又a≤$\frac{1}{4}$,
所以a≤$\frac{1}{4}$;
由f′(x)≥0,由x∈[$\frac{1}{2}$,2],得a≥$\frac{1}{{x}^{2}}$,得到a≥4,此时f(x)在区间[$\frac{1}{2}$,2]上为增函数,
要使对任意的实数b,都存在实数x0∈[$\frac{1}{2}$,2],使得不等式|f(x0)|≥$\frac{1}{2}$成立,
只要f(x0)≥$\frac{1}{2}$或者f(x0)≤-$\frac{1}{2}$
所以只要f(x)的最大值为f(2)=$\frac{1}{2}$+2a+b$≥\frac{1}{2}$或者f($\frac{1}{2}$)=2+$\frac{1}{2}$a+b$≤-\frac{1}{2}$.
解得a≥$\frac{5}{3}$,又a≥4,
所以a≥4;
综上a≥4或者a≤$\frac{1}{4}$.
点评 本题考查函数的单调性,最值与导数的关系,和存在性问题的转化,属于压轴题,难题

 2011年3月11日,日本发生了9.0级大地震,同时导致了福岛核电站的泄露事件,给环境带来的一定的污染,也给世界各国的人们对环境的保护敲响了警钟.根据空气质量指数API(为整数)的不同,可将空气质量分级如表:
2011年3月11日,日本发生了9.0级大地震,同时导致了福岛核电站的泄露事件,给环境带来的一定的污染,也给世界各国的人们对环境的保护敲响了警钟.根据空气质量指数API(为整数)的不同,可将空气质量分级如表:| API | 0~50 | 51~200 | 101~150 | 151~200 | 201~250 | 251~300 | >300 |
| 级别 | Ⅰ | Ⅱ | Ⅲ1 | Ⅲ2 | Ⅳ1 | Ⅳ2 | Ⅴ |
| 状况 | 优 | 良 | 轻微污染 | 轻度污染 | 中度污染 | 中度重污染 | 重度污染 |
(1)求直方图中x的值;
(2)计算一年中空气质量为良和轻微污染的总天数;
(3)求该城市一年中每天空气质量不为良且不为轻微污染的概率.
| A. | $\frac{π}{4}$ | B. | $\frac{π}{3}$ | C. | $\frac{π}{2}$ | D. | $\frac{2π}{3}$ |
| A. | 双曲线$\frac{{x}^{2}}{25}$-$\frac{{y}^{2}}{9}$=1与椭圆$\frac{{x}^{2}}{35}$+y2=1有相同的焦点 | |
| B. | “0<x<2”是“x2-2x-3<0”充分不必要条件 | |
| C. | “若xy=0,则x、y中至少有一个为0”的否命题是真命题. | |
| D. | “?x∈R,使x2-2x+3≤0” |
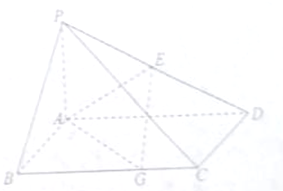 如图,在四棱锥P-ABCD中,底圆ABCD是矩形,PA⊥平面ABCD,PA=AB=2,BC=4,E是PD的中点,点G在线段BC上,且BG=3.
如图,在四棱锥P-ABCD中,底圆ABCD是矩形,PA⊥平面ABCD,PA=AB=2,BC=4,E是PD的中点,点G在线段BC上,且BG=3. 如图,在四棱锥O-ABCD中,底面ABCD是边长为2的正方形,OA⊥底面ABCD,OA=2,M为OA的中点.则异面直线OB与MD所成角余弦值为$\frac{\sqrt{10}}{10}$.
如图,在四棱锥O-ABCD中,底面ABCD是边长为2的正方形,OA⊥底面ABCD,OA=2,M为OA的中点.则异面直线OB与MD所成角余弦值为$\frac{\sqrt{10}}{10}$.