题目内容
4.已知函数f(x)=cos(2x+$\frac{π}{3}$)+2sin2x.求f(x)在[-π,0]上的单调递减区间.分析 由条件利用三角恒等变换化简f(x)的解析式,再利用正弦函数的单调性,求得f(x)在[-π,0]上的单调递减区间.
解答 解:∵函数f(x)=cos(2x+$\frac{π}{3}$)+2sin2x=$\frac{1}{2}$cos2x-$\frac{\sqrt{3}}{2}$sin2x+2•$\frac{1-cos2x}{2}$
=-$\frac{1}{2}$cos2x-$\frac{\sqrt{3}}{2}$sin2x+1=-sin(2x+$\frac{π}{6}$)+1,
令2kπ-$\frac{π}{2}$≤2x+$\frac{π}{6}$≤2kπ+$\frac{π}{2}$,k∈z,求得kπ-$\frac{π}{3}$≤x≤kπ+$\frac{π}{6}$,
可得函数f(x)的减区间为[kπ-$\frac{π}{3}$,kπ+$\frac{π}{6}$],k∈z.
再结合x∈[-π,0],可得f(x)在[-π,0]上的单调递减区间为[-π,-$\frac{5π}{6}$]、[-$\frac{π}{3}$,0].
点评 本题主要考查三角恒等变换,正弦函数的单调性,属于基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
15.执行如图所示的程序框图,输出的结果为( )
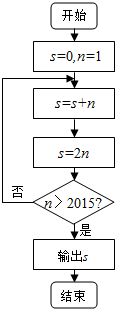

| A. | 210-1 | B. | 211-1 | C. | 21007-1 | D. | 21024-1 |
12.在极坐标系中,曲线C:ρ=2sinθ,A、B为曲线C的两点,以极点为原点,极轴为x轴非负半轴的直角坐标中,曲线E:$\left\{{\begin{array}{l}{x=4t+2}\\{y=-3t-3}\end{array}}\right.$上一点P,则∠APB的最大值为( )
| A. | $\frac{π}{4}$ | B. | $\frac{π}{3}$ | C. | $\frac{π}{2}$ | D. | $\frac{2π}{3}$ |
19.已知抛物线y=ax2+bx+c(a≠0)的对称轴在y轴的左侧,其中a、b、c∈{-3,-2,-1,0,1,2,3},在这些抛物线中,记随机变量X=|a-b|,则X的均值EX为( )
| A. | $\frac{8}{9}$ | B. | $\frac{3}{5}$ | C. | $\frac{2}{5}$ | D. | $\frac{1}{3}$ |

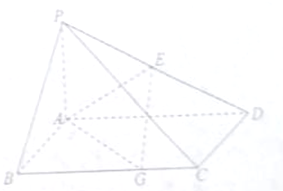 如图,在四棱锥P-ABCD中,底圆ABCD是矩形,PA⊥平面ABCD,PA=AB=2,BC=4,E是PD的中点,点G在线段BC上,且BG=3.
如图,在四棱锥P-ABCD中,底圆ABCD是矩形,PA⊥平面ABCD,PA=AB=2,BC=4,E是PD的中点,点G在线段BC上,且BG=3. 如图,在四棱锥O-ABCD中,底面ABCD是边长为2的正方形,OA⊥底面ABCD,OA=2,M为OA的中点.则异面直线OB与MD所成角余弦值为$\frac{\sqrt{10}}{10}$.
如图,在四棱锥O-ABCD中,底面ABCD是边长为2的正方形,OA⊥底面ABCD,OA=2,M为OA的中点.则异面直线OB与MD所成角余弦值为$\frac{\sqrt{10}}{10}$.