题目内容
【题目】如图,在多面体![]() 中,底面
中,底面![]() 是边长为
是边长为![]() 的菱形,
的菱形, ![]() ,四边形
,四边形![]() 是矩形,平面
是矩形,平面![]() 平面
平面![]() ,
, ![]() ,
, ![]() 是
是![]() 的中点.
的中点.

(1)求证: ![]() 平面
平面![]() ;
;
(2)求直线![]() 与平面
与平面![]() 所成角的正弦值;
所成角的正弦值;
(3)求二面角![]() 的大小.
的大小.
【答案】(1)见解析;(2)![]() ;(3)
;(3)![]() .
.
【解析】试题分析:(1)由平面![]() 平面
平面![]() ,及
,及![]() ,得
,得![]() 平面
平面![]() (平面与平面垂直的性质);(2)建立适当的空间直角坐标系,求得平面
(平面与平面垂直的性质);(2)建立适当的空间直角坐标系,求得平面![]() 的法向量的坐标及
的法向量的坐标及![]() ,可得
,可得![]() 与平面
与平面![]() 所成角的夹角的正弦值;(3)由(2)的空间直角坐标,可求得
所成角的夹角的正弦值;(3)由(2)的空间直角坐标,可求得![]() 的法向量
的法向量![]() ,平面
,平面![]() 的法向量
的法向量![]() ,得
,得![]() ,由二面角为锐角,得所求二面角的值。
,由二面角为锐角,得所求二面角的值。
(1)证明:因为四边形![]() 是菱形,所以
是菱形,所以![]() .
.
因为平面![]() 平面
平面![]() ,且四边形
,且四边形![]() 是矩形,所以
是矩形,所以![]() 平面
平面![]() ,
,
又因为![]() 平面
平面![]() ,所以
,所以![]() .
.
因为![]() ,所以
,所以![]() 平面
平面![]() .
.
(2)设![]() ,取
,取![]() 的中点
的中点![]() ,连接
,连接![]() ,
,
因为四边形![]() 是矩形,
是矩形, ![]() 分别为
分别为![]() ,
, ![]() 的中点,所以
的中点,所以![]() ,
,
又因为![]() 平面
平面![]() ,所以
,所以![]() 平面
平面![]() ,
,
由![]() ,得
,得![]() 两两垂直,所以以
两两垂直,所以以![]() 为原点,
为原点, ![]() 所在直线分别为
所在直线分别为![]() 轴,
轴, ![]() 轴,
轴, ![]() 轴,如图建立空间直角坐标系.
轴,如图建立空间直角坐标系.
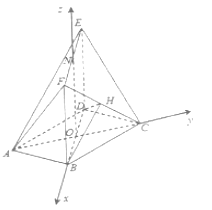
因为底面![]() 是边长为
是边长为![]() 的菱形,
的菱形, ![]() ,
, ![]() ,
,
所以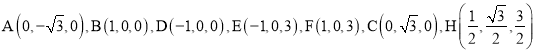 .
.
因为![]() 平面
平面![]() ,所以平面
,所以平面![]() 的法向量
的法向量![]() .
.
设直线![]() 与平面
与平面![]() 所成角为
所成角为![]() ,由
,由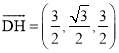 ,得
,得
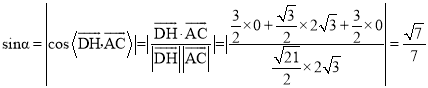 ,
,
所以直线![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() .
.
(3)由(2)得, 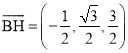 ,
, ![]() ,
,
设平面![]() 的法向量为
的法向量为![]() ,
,
所以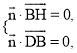 即
即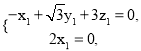
令![]() ,得
,得![]() ,由
,由![]() 平面
平面![]() ,得平面
,得平面![]() 的法向量为
的法向量为![]() ,
,
则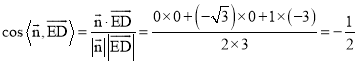 ,
,
由图可知二面角![]() 为锐角,
为锐角,
所以二面角![]() 的大小为
的大小为![]() .
.

练习册系列答案
相关题目
【题目】某种产品的广告费支出![]() (百万元)与销售额
(百万元)与销售额![]() (百万元)之间有如下对应数据:
(百万元)之间有如下对应数据:
| 2 | 4 | 5 | 6 | 8 |
| 30 | 40 | 50 | 60 | 70 |
如果![]() 与
与![]() 之间具有线性相关关系.
之间具有线性相关关系.
(1)作出这些数据的散点图;
(2)求这些数据的线性回归方程![]() ;
;
(3)预测当广告费支出为9百万元时的销售额。 ( 参考数据: ![]() )
)