题目内容
【题目】(本题满分14分)如图,已知椭圆![]() :
:![]() ,其左右焦点为
,其左右焦点为![]() 及
及![]() ,过点
,过点![]() 的直线交椭圆
的直线交椭圆![]() 于
于![]() 两点,线段
两点,线段![]() 的中点为
的中点为![]() ,
,![]() 的中垂线与
的中垂线与![]() 轴和
轴和![]() 轴分别交于
轴分别交于![]() 两点,且
两点,且![]() 、
、![]() 、
、![]() 构成等差数列.
构成等差数列.
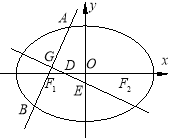
(1)求椭圆![]() 的方程;
的方程;
(2)记△![]() 的面积为
的面积为![]() ,△
,△![]() (
(![]() 为原点)的面积为
为原点)的面积为![]() .试问:是否存在直线
.试问:是否存在直线![]() ,使得
,使得![]() ?说明理由.
?说明理由.
【答案】(1)![]() ;(2)不存在直线
;(2)不存在直线![]() ,使得
,使得 ![]() .
.
【解析】
试题分析:(1)求椭圆![]() 的标准方程,由已知
的标准方程,由已知![]() 、
、![]() 、
、![]() 构成等差数列,即
构成等差数列,即![]() ,由椭圆的定义可得,
,由椭圆的定义可得,![]() ,由已知焦点为
,由已知焦点为![]() 及
及![]() ,可得
,可得![]() ,可求出
,可求出![]() ,从而得椭圆
,从而得椭圆![]() 的标准方程;(2)记△
的标准方程;(2)记△![]() 的面积为
的面积为![]() ,△
,△![]() (
(![]() 为原点)的面积为
为原点)的面积为![]() .试问:是否存在直线
.试问:是否存在直线![]() ,使得
,使得![]() ?说明理由,这是探索性命题,一般假设其存在,本题假设存在直线
?说明理由,这是探索性命题,一般假设其存在,本题假设存在直线![]() ,使得
,使得 ![]() ,由题意直线
,由题意直线![]() 不能与
不能与![]() 轴垂直,故设
轴垂直,故设![]() 方程为
方程为![]() ,将其代入
,将其代入![]() ,整理得
,整理得 ![]() ,设
,设![]() ,
,![]() ,由根与系数关系,表示出点
,由根与系数关系,表示出点![]() 的坐标,写出中垂线方程,得点
的坐标,写出中垂线方程,得点![]() 的坐标,由于
的坐标,由于![]() 和
和![]() 相似,若
相似,若![]() ,则
,则![]() ,建立方程,求解斜率
,建立方程,求解斜率![]() 的值,若有解,则存在,若无解,则不存在.
的值,若有解,则存在,若无解,则不存在.
试题解析:(1)因为![]() 、
、![]() 、
、![]() 构成等差数列,
构成等差数列,
所以![]() ,所以
,所以![]() . (2分)
. (2分)
又因为![]() ,所以
,所以![]() , (3分)
, (3分)
所以椭圆![]() 的方程为
的方程为![]() . (4分)
. (4分)
(2)假设存在直线![]() ,使得
,使得 ![]() ,显然直线
,显然直线![]() 不能与
不能与![]() 轴垂直.
轴垂直.
设![]() 方程为
方程为![]() (5分)
(5分)
将其代入![]() ,整理得
,整理得 ![]() (6分)
(6分)
设![]() ,
,![]() ,所以
,所以 ![]() .
.
故点![]() 的横坐标为
的横坐标为![]() .所以
.所以 ![]() . (8分)
. (8分)
因为 ![]() ,所以
,所以 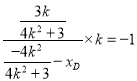 , 解得
, 解得 ![]() ,
,
即 ![]() (10分)
(10分)
![]() 和
和![]() 相似,
相似,![]() 若
若![]() ,则
,则![]() (11分)
(11分)
所以 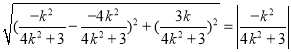 , (12分)
, (12分)
整理得 ![]() . (13分)
. (13分)
因为此方程无解,所以不存在直线![]() ,使得
,使得 ![]() . (14分)
. (14分)

【题目】某研究性学习小组为了调查研究学生玩手机对学习的影响,现抽取了30名学生,得到数据如表:
玩手机 | 不玩手机 | 合计 | |
学习成绩优秀 | 8 | ||
学习成绩不优秀 | 16 | ||
合计 | 30 |
已知在全部的30人中随机抽取1人,抽到不玩手机的概率为![]() .
.
(1)请将2×2列联表补充完整;
(2)能否在犯错误的概率不超过0.005的前提下认为玩手机对学习有影响;
(3)现从不玩手机,学习成绩优秀的8名学生中任意选取两人,对他们的学习情况进行全程跟踪,记甲、乙两名学生被抽到的人数为X,求X的分布列和数学期望.
附:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
![]() .
.
【题目】某品牌手机厂商推出新款的旗舰机型,并在某地区跟踪调查得到这款手机上市时间(![]() 个月)和市场占有率(
个月)和市场占有率(![]() )的几组相关对应数据:
)的几组相关对应数据:
| 1 | 2 | 3 | 4 | 5 |
| 0.02 | 0.05 | 0.1 | 0.15 | 0.18 |
(1)根据上表中的数据,用最小二乘法求出![]() 关于
关于![]() 的线性回归方程;
的线性回归方程;
(2)根据上述回归方程,分析该款旗舰机型市场占有率的变化趋势,并预测自上市起经过多少个月,该款旗舰机型市场占有率能超过![]() (精确到月).
(精确到月).