题目内容
【题目】设函数
，函数
在区间
上的最大值为
.
（1）若
，求的值；
（2）若
对任意的
恒成立，求
的最大值.
【答案】（1）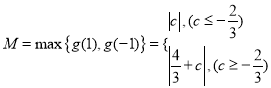
；（2）
.
【解析】
试题（1）根据
可知该函数是对勾函数作了左右和上下的平移变换，若
，则可得到
在区间
上是增函数，故
的最大值就是
，但是
，
的图像是由的图像作了翻折变换，上不动而下翻折，要比较
与
两者的大小，所以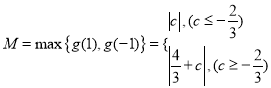；（2）第二小题由于不能确定在区间上是递增的还是先减后增，因此要分类讨论，一种情况是是递增的，最大值在
中产生，另一种情况是先减后增，最大值在
或是
中产生，通过三种情况分类，最后总结得到
的最小值，也就是
的最大值.
试题解析：解：（1）当时，在区间上是增函数，
所以
，
所以.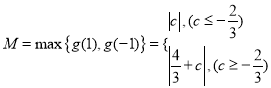
（2）①当
时，因为
，
，
所以
，所以
.
②当
时，有
，
则
，
，所以
.
③当
时，有
，
则
，
所以
，所以.
综上可知，对任意的
都有.
练习册系列答案
相关题目
