题目内容
【题目】已知函数![]() .
.
(1)若![]() ,
,![]() ,求
,求![]() 的最大值;
的最大值;
(2)当![]() 时,讨论
时,讨论![]() 极值点的个数.
极值点的个数.
【答案】(1)![]() (2)
(2)![]() 时,
时,![]() 极值点的个数为0个;
极值点的个数为0个;![]() 时,
时,![]() 极值点的个数为2个
极值点的个数为2个
【解析】
(1)利用导数求出单调性,从而求得![]() 的最大值;
的最大值;
(2)先求导数,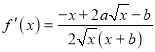 ,导数的符号由分子
,导数的符号由分子![]() 确定,先分
确定,先分![]() 和
和![]() 讨论,
讨论,![]() 时,易得
时,易得![]() ,当
,当![]() 时,将
时,将![]() 看成关于
看成关于![]() 的二次函数,由
的二次函数,由![]() 确定
确定![]() 的符号,从而判断极值点的个数.
的符号,从而判断极值点的个数.
(1)当![]() ,
,![]() 时,
时,![]() ,
,
此时,函数![]() 定义域为
定义域为![]() ,
,![]() ,
,
由![]() 得:
得:![]() ;由
;由![]() 得:
得:![]() ,
,
所以![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减.
上单调递减.
所以![]() .
.
(2)当![]() 时,函数
时,函数![]() 定义域为
定义域为![]() ,
,
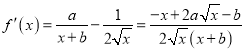 ,
,
①当![]() 时,
时,![]() 对任意的
对任意的![]() 恒成立,
恒成立,
![]() 在
在![]() 上单调递减,所以此时
上单调递减,所以此时![]() 极值点的个数为0个;
极值点的个数为0个;
②当![]() 时,设
时,设![]() ,
,
(i)当![]() ,即
,即![]() 时,
时,
![]() 对任意的
对任意的![]() 恒成立,即
恒成立,即![]() 在
在![]() 上单调递减,
上单调递减,
所以此时![]() 极值点的个数为0个;
极值点的个数为0个;
(ii)当![]() ,即
,即![]() 时,记方程
时,记方程![]() 的两根分别为
的两根分别为![]() ,
,![]() ,
,
则![]() ,
,![]() ,所以
,所以![]() ,
,![]() 都大于0,
都大于0,
即![]() 在
在![]() 上有2个左右异号的零点,
上有2个左右异号的零点,
所以此时![]() 极值点的个数为2.
极值点的个数为2.
综上所述![]() 时,
时,![]() 极值点的个数为0个;
极值点的个数为0个;
![]() 时,
时,![]() 极值点的个数为2个.
极值点的个数为2个.

练习册系列答案
 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案
相关题目
【题目】已知x与y之间的几组数据如表:
x | 1 | 2 | 3 | 4 |
y | 1 | m | n | 4 |
如表数据中y的平均值为2.5,若某同学对m赋了三个值分别为1.5,2,2.5,得到三条线性回归直线方程分别为![]() ,
,![]() ,
,![]() ,对应的相关系数分别为
,对应的相关系数分别为![]() ,
,![]() ,
,![]() ,下列结论中错误的是( )
,下列结论中错误的是( )
参考公式:线性回归方程![]() 中,其中
中,其中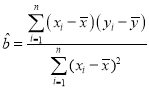 ,
,![]() .相关系数
.相关系数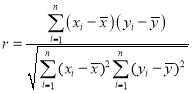 .
.
A.三条回归直线有共同交点B.相关系数中,![]() 最大
最大
C.![]() D.
D.![]()