题目内容
若直角 的内切圆与斜边
的内切圆与斜边 相切于点
相切于点 ,且
,且 ,则
,则 的面积为_________.
的面积为_________.
 的内切圆与斜边
的内切圆与斜边 相切于点
相切于点 ,且
,且 ,则
,则 的面积为_________.
的面积为_________.2
解:
连接内心和直角三角形的各个顶点,设直角三角形的两条直角边是a,b.则直角三角形的面积是a+b+c2r;又直角三角形内切圆的半径r=a+b-c/2,则a+b=2r+c,所以直角三角形的面积是r(r+c);因为内切圆的面积是πr2,则它们的比是πr/c+r.,斜边长为3,内切圆半径为1/2,则可得其面积为2
连接内心和直角三角形的各个顶点,设直角三角形的两条直角边是a,b.则直角三角形的面积是a+b+c2r;又直角三角形内切圆的半径r=a+b-c/2,则a+b=2r+c,所以直角三角形的面积是r(r+c);因为内切圆的面积是πr2,则它们的比是πr/c+r.,斜边长为3,内切圆半径为1/2,则可得其面积为2

练习册系列答案
 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案
相关题目
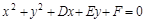 与
与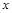 轴的两个交点分别位于原点的两侧,则有( )
轴的两个交点分别位于原点的两侧,则有( )
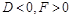


 ,
, 为圆内异于
为圆内异于 是圆周上一动点,把纸片折叠使
是圆周上一动点,把纸片折叠使 ,设
,设 交于
交于 ,则
,则
 ,各段弧所在的圆经过同一点
,各段弧所在的圆经过同一点 (点
(点 段弧所对的圆心角为
段弧所对的圆心角为 ,则
,则 ____________ .
____________ .
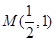 的直线
的直线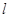 与圆C:
与圆C: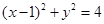 交于
交于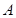 、
、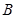 两点,
两点,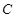 为圆心,当
为圆心,当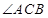 最小时,直线
最小时,直线 上运动,
上运动,





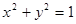

 为圆上一动点,点
为圆上一动点,点 在
在 上,点
上,点 在
在 上,且满足
上,且满足 的轨迹为曲线
的轨迹为曲线 .
. 与(1)中所求点
与(1)中所求点 是坐标原点,且
是坐标原点,且 ,求△
,求△ 的面积的取值范围.
的面积的取值范围.