题目内容
过点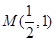 的直线
的直线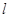 与圆C:
与圆C: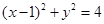 交于
交于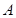 、
、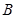 两点,
两点,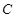 为圆心,当
为圆心,当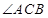 最小时,直线
最小时,直线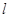 的方程为_________________.
的方程为_________________.
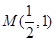 的直线
的直线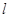 与圆C:
与圆C: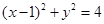 交于
交于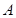 、
、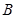 两点,
两点,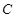 为圆心,当
为圆心,当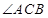 最小时,直线
最小时,直线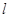 的方程为_________________.
的方程为_________________.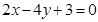 (或
(或 等)
等)分析:研究知点M(1/2,1)在圆内,过它的直线与圆交于两点A,B,当∠ACB最小时,直线l与CM垂直,故先求直线CM的斜率,再根据充要条件求出直线l的斜率,由点斜式写出其方程。
解答:
验证知点M(1/2,1)在圆内,
当∠ACB最小时,直线l与CM垂直,
由圆的方程,圆心C(1,0)
∵kCM=(1-0)/(1/2-1)=-2,
∴l:(y-1)=1/2(x -1/2),整理得2x-4y+3=0。
点评:本题考点是直线与圆的位置关系,考查到了线线垂直时斜率之积为-1,以及用点斜式写出直线的方程。

练习册系列答案
相关题目
 经过点
经过点 ,对称轴为坐标轴,焦点
,对称轴为坐标轴,焦点 在
在 轴上,离心率
轴上,离心率 .
. 的角平分线所在直线
的角平分线所在直线 的方程;
的方程;
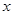 轴相切,圆心在直线
轴相切,圆心在直线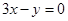 上,且被直线
上,且被直线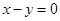 截得的弦长为
截得的弦长为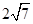 的圆的方程。
的圆的方程。 与圆
与圆 的两个交点,则
的两个交点,则


 的内切圆与斜边
的内切圆与斜边 相切于点
相切于点 ,且
,且 ,则
,则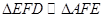 ;
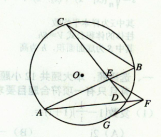
;
 的距离为
的距离为 ,求该圆的方程.
,求该圆的方程. 及
及 都相切,圆心在直线
都相切,圆心在直线 上,则圆C的方程为________________________。
上,则圆C的方程为________________________。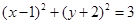 的一条弦的中点为
的一条弦的中点为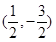 ,这条弦所在的直线方程为______
,这条弦所在的直线方程为______