题目内容
如题（15）图，图中的实线是由三段圆弧连接而成的一条封闭曲线
，各段弧所在的圆经过同一点
（点不在上）且半径相等. 设第
段弧所对的圆心角为
，则
____________ .
，各段弧所在的圆经过同一点（点不在上）且半径相等. 设第段弧所对的圆心角为，则____________ .
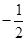
解：
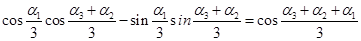
可令同过P点的三圆的交点分别是A，B，C，连接PA，PB，PC，可得得出∠APB+∠APC+∠BPC=2π
因为在各个圆的半径相等，故此三角的大小皆为2π /3由于在圆中同弦所对的圆周角互补，故在各个圆中，AB，BC，CA所与三角相对的圆周角为π /3
故AB，BC，CA所对的圆心角是2π/ 3 ，
又α1+α2+α3=4π，所以cos(α 1 +α 2 +α 3 / 3 )="-1" /2 ．
练习册系列答案
相关题目
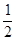
的圆心是双曲线
的一个焦点，则此双曲线的渐近线方程为 .
两点，动点
不在
轴上，且满足
其中
为原点，则
的内切圆与斜边
相切于点
,且
,则
的参数方程是
（t是参数）圆C的极坐标方程为
.
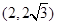在双曲线
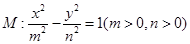上，圆C：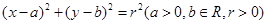
与双曲线M的一条渐近线相切于点（1，2），且圆C被x轴截得的弦长为4.（Ⅰ）求双曲线M的方程；（Ⅱ）求圆C的方程；（Ⅲ）过圆C内一定点Q（s，t）（不同于点C）任作一条直线与圆C相交于点A、B，以A、B为切点分别作圆C的切线PA、PB，求证：点P在定直线l上，并求出直线l的方程.
