题目内容
设函数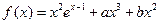 ,已知
,已知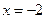 和
和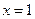 为
为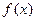 的极值点.
的极值点.
(Ⅰ)求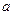 和
和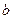 的值;
的值;
(Ⅱ)讨论函数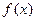 的单调性;
的单调性;
(Ⅲ)设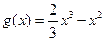 ,比较
,比较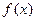 与
与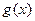 的大小.
的大小.
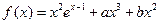 ,已知
,已知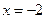 和
和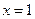 为
为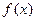 的极值点.
的极值点.(Ⅰ)求
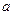 和
和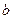 的值;
的值;(Ⅱ)讨论函数
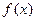 的单调性;
的单调性;(Ⅲ)设
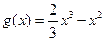 ,比较
,比较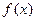 与
与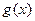 的大小.
的大小.(1)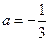 ,
,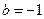 .
.
(2)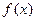 在
在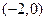 和
和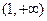 上是单调递增的;在
上是单调递增的;在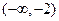 和
和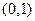 上是单调递减的.
上是单调递减的.
(3)(1)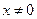 且
且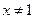 时
时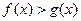
(2)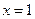 或
或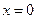 时,
时,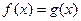
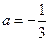 ,
,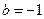 .
.(2)
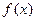 在
在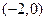 和
和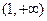 上是单调递增的;在
上是单调递增的;在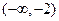 和
和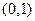 上是单调递减的.
上是单调递减的.(3)(1)
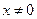 且
且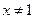 时
时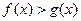
(2)
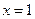 或
或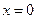 时,
时,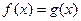
(Ⅰ)因为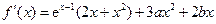
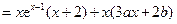 ,
,
又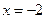 和
和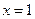 为
为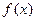 的极值点,所以
的极值点,所以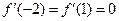 ,
,
因此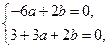 解该方程组得
解该方程组得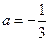 ,
,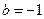 .
.
(Ⅱ)因为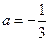 ,
,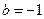 ,所以
,所以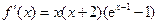 ,
,
令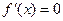 ,解得
,解得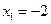 ,
,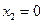 ,
, .
.
因为当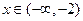
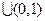 时,
时,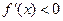 ;
;
当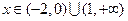 时,
时,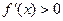 .
.
所以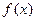 在
在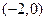 和
和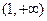 上是单调递增的;在
上是单调递增的;在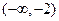 和
和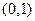 上是单调递减的.
上是单调递减的.
(Ⅲ)由(Ⅰ)可知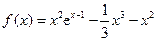 ,
,
故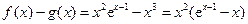 ,令
,令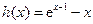 ,则
,则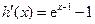 .
.
令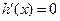 ,得
,得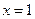 ,因为
,因为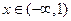 时,
时,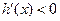 ,
,
所以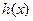 在
在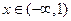 上单调递减.故
上单调递减.故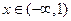 时,
时,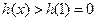 ;
;
因为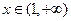 时,
时,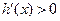 ,所以
,所以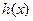 在
在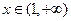 上单调递增.
上单调递增.
故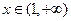 时,
时,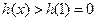 .
.
所以对任意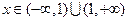 ,恒有
,恒有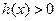 ,又
,又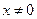 时,
时,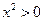 ,
,
因此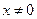 且
且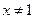 时
时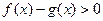 ,
,
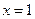 或
或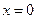 时
时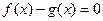 ,
,
所以, (1)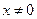 且
且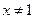 时
时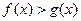
(2)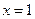 或
或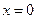 时,
时,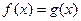
【注:】按以下做法不扣分(以下是高考命题人给的原解)这种解法不太严谨,但也被大部分人所接受
(Ⅲ)由(Ⅰ)可知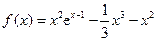 ,
,
故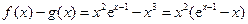 ,令
,令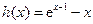 ,则
,则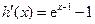 .
.
令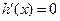 ,得
,得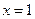 ,因为
,因为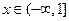 时,
时,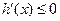 ,
,
所以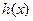 在
在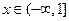 上单调递减.故
上单调递减.故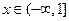 时,
时,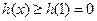 ;
;
因为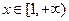 时,
时,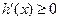 ,所以
,所以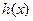 在
在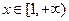 上单调递增.
上单调递增.
故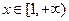 时,
时,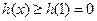 .
.
所以对任意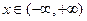 ,恒有
,恒有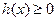 ,又
,又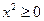 ,因此
,因此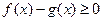 ,
,
故对任意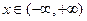 ,恒有
,恒有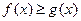
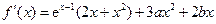
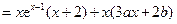 ,
,又
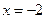 和
和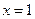 为
为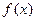 的极值点,所以
的极值点,所以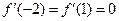 ,
,因此
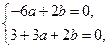 解该方程组得
解该方程组得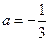 ,
,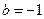 .
.(Ⅱ)因为
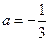 ,
,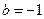 ,所以
,所以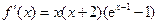 ,
,令
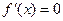 ,解得
,解得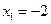 ,
,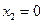 ,
, .
.因为当
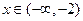
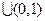 时,
时,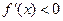 ;
;当
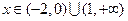 时,
时,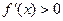 .
.所以
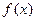 在
在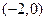 和
和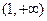 上是单调递增的;在
上是单调递增的;在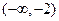 和
和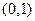 上是单调递减的.
上是单调递减的.(Ⅲ)由(Ⅰ)可知
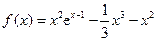 ,
,故
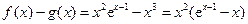 ,令
,令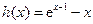 ,则
,则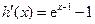 .
.令
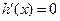 ,得
,得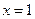 ,因为
,因为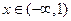 时,
时,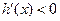 ,
,所以
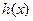 在
在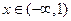 上单调递减.故
上单调递减.故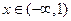 时,
时,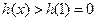 ;
;因为
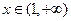 时,
时,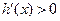 ,所以
,所以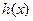 在
在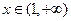 上单调递增.
上单调递增.故
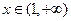 时,
时,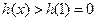 .
.所以对任意
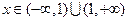 ,恒有
,恒有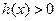 ,又
,又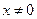 时,
时,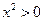 ,
,因此
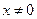 且
且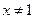 时
时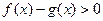 ,
,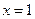 或
或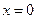 时
时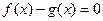 ,
,所以, (1)
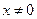 且
且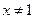 时
时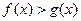
(2)
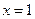 或
或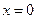 时,
时,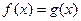
【注:】按以下做法不扣分(以下是高考命题人给的原解)这种解法不太严谨,但也被大部分人所接受
(Ⅲ)由(Ⅰ)可知
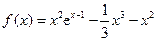 ,
,故
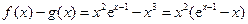 ,令
,令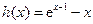 ,则
,则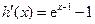 .
.令
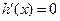 ,得
,得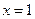 ,因为
,因为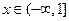 时,
时,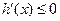 ,
,所以
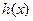 在
在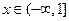 上单调递减.故
上单调递减.故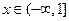 时,
时,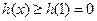 ;
;因为
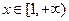 时,
时,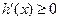 ,所以
,所以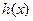 在
在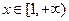 上单调递增.
上单调递增.故
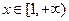 时,
时,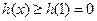 .
.所以对任意
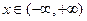 ,恒有
,恒有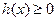 ,又
,又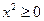 ,因此
,因此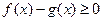 ,
,故对任意
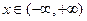 ,恒有
,恒有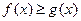

练习册系列答案
 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案
相关题目
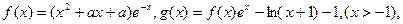
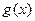 的单调区间,并证明此时方程
的单调区间,并证明此时方程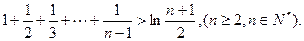
 当
当 时取得极大值。当
时取得极大值。当 时取得极小值,则
时取得极小值,则 的取值范围是( )
的取值范围是( )



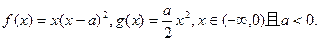
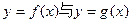 的图象的交点A的坐标;
的图象的交点A的坐标;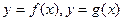 的图象在交点A处的切线分别为
的图象在交点A处的切线分别为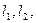 是否存在这样的实数a,使得
是否存在这样的实数a,使得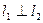 ?若存在,请求出a的值和相应的点A坐标;若不存在,请说明理由。
?若存在,请求出a的值和相应的点A坐标;若不存在,请说明理由。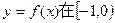 上最小值为F(a),求
上最小值为F(a),求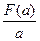 的最小值。
的最小值。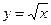 在
在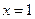 处的导数;
处的导数;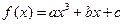
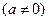 为奇函数,其图象在点
为奇函数,其图象在点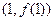 处的切线与直线
处的切线与直线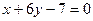 垂直,且在x=-1处取得极值.
垂直,且在x=-1处取得极值.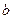 ,
,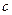 的值;
的值;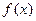 在
在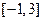 上的最大值和最小值。
上的最大值和最小值。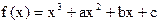 ,曲线
,曲线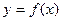 在点x=1处的切线l不过第四象限且斜率为3,又坐标原点到切线l的距离为
在点x=1处的切线l不过第四象限且斜率为3,又坐标原点到切线l的距离为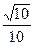 ,若
,若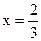 时,
时,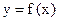 有极值.
有极值.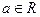 ,
,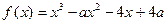 .
.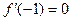 ,求函数
,求函数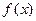 在区间
在区间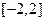 的最大值与最小值;
的最大值与最小值;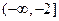 和
和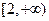 上都是增函数,求实数
上都是增函数,求实数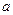 的取值范围.
的取值范围.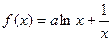 .
.
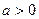 时,求函数
时,求函数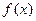 的单调区间和极值;
的单调区间和极值;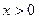 ,均有
,均有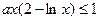 ,求实数
,求实数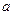 的取值范围;
的取值范围;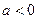 ,对任意
,对任意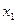 、
、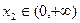 ,且
,且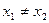 ,试比较
,试比较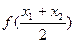 与
与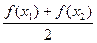 的大小.
的大小.