Question

【题目】已知抛物线：，圆：.

（1）若过抛物线的焦点的直线与圆相切，求直线方程；

（2）在（1）的条件下，若直线交抛物线于，两点，轴上是否存在点使（为坐标原点）？若存在，求出点的坐标；若不存在，请说明理由.

Answer 1

【答案】（1）切线方程为或.（2）见解析

【解析】

（1）先求得抛物线的焦点，根据点斜式设出直线的方程，利用圆心到直线的距离等于半径，求出直线的方程.（2）联立直线的方程和抛物线的方程，化简后写出韦达定理，根据，则列方程，解方程求得的值，进而求得点的坐标.

解：（1）由题知抛物线的焦点为，

当直线的斜率不存在时，过点的直线不可能与圆相切；

所以过抛物线焦点与圆相切的直线的斜率存在，

设直线斜率为，则所求的直线方程为，即，

所以圆心到直线的距离为，

当直线与圆相切时，有，

所以所求的切线方程为或.

（2）由（1）知，不妨设直线：，交抛物线于，两点，

联立方程组，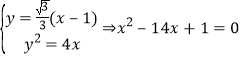

所以，，

假设存在点使，

则.

而，，

所以

，

即，

故存在点符合条件.

当直线：时，

由对称性易知点也符合条件.

综合可知在（1）的条件下，存在点使.