题目内容
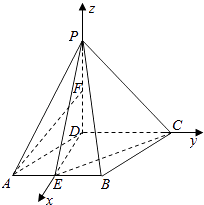
【题目】如图,在四棱锥P﹣ABCD中,底面ABCD是菱形,∠DAB=60°,PD⊥平面ABCD,PD=AD=1,点E,F分别为AB和PD中点. (Ⅰ)求证:直线AF∥平面PEC;
(Ⅱ)求PC与平面PAB所成角的正弦值.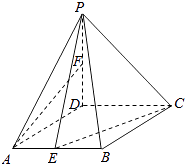
【答案】解:(Ⅰ)证明:作FM∥CD交PC于M. ∵点F为PD中点,
∴ ![]() .
.
∵点E为AB的中点.
∴ ![]() ,
,
又AE∥FM,
∴四边形AEMF为平行四边形,
∴AF∥EM,
∵AF平面PEC,EM平面PEC,
∴直线AF∥平面PEC.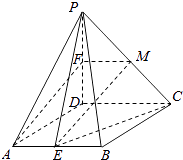
(Ⅱ)已知∠DAB=60°,
进一步求得:DE⊥DC,
则:建立空间直角坐标系,
则 P(0,0,1),C(0,1,0),E( ![]() ,0,0),
,0,0),
A( ![]() ,﹣
,﹣ ![]() ,0),B(
,0),B( ![]() ,
, ![]() ,0).
,0).
所以: 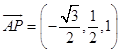 ,
, ![]() .
.
设平面PAB的一个法向量为: ![]() ,.
,.
∵ 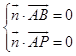 ,
,
则: 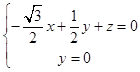 ,
,
解得: 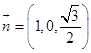 ,
,
所以平面PAB的法向量为: 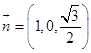
∵ ![]() ,
,
∴设向量 ![]() 和
和 ![]() 的夹角为θ,
的夹角为θ,
∴cosθ= 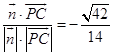 ,
,
∴PC平面PAB所成角的正弦值为 ![]() .
.
【解析】(Ⅰ)首先利用中点引出中位线,进一步得到线线平行,再利用线面平行的判定定理得到结论.(Ⅱ)根据直线间的两两垂直,尽力空间直角坐标系,再求出平面PAB的法向量,最后利用向量的数量积求出线面的夹角的正弦值.
【考点精析】通过灵活运用直线与平面平行的判定和空间角的异面直线所成的角,掌握平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行;简记为:线线平行,则线面平行;已知![]() 为两异面直线,A,C与B,D分别是
为两异面直线,A,C与B,D分别是![]() 上的任意两点,
上的任意两点,![]() 所成的角为,则
所成的角为,则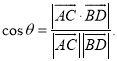 即可以解答此题.
即可以解答此题.

练习册系列答案
 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案
相关题目
