题目内容
【题目】如图，斜率为1的直线过抛物线y2=2px（p＞0）的焦点，与抛物线交于两点A、B，M为抛物线 
上的动点． 
（1）若|AB|=8，求抛物线的方程；
（2）求S△ABM的最大值．
【答案】
（1）解：由条件知 
，则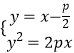 
，
消去y得： 
，
则x1+x2=3p，由抛物线定义得|AB|=x1+x2+p=4p
又因为|AB|=8，即p=2，则抛物线的方程为y2=4x
（2）解：由（1）知|AB|=4p和 ，设 
，
则M到AB的距离为： 
，
因点M在直线AB的上方，所以 
则 
由 知 
所以 
，则当y0=p时， 
则 
【解析】（1）先联立直线方程和抛物线方程，得到x1+x2的值，再根据抛物线定义，得到焦点弦的弦长公式， 代入并解得p，从而求得抛物线的方程为y2=4x．（2）设 ，根据直线AB的方程得到用y0和p表示的点M到AB的距离d．又根据点M在直线AB的上方
解得y0的范围，即求出了d的最大值，再代入面积公式，可求得S△ABM的最大值．
练习册系列答案
阅读快车系列答案
相关题目
