Question

【题目】已知点是抛物线的焦点，是抛物线在第一象限内的点，且，

(I) 求点的坐标；

(II)以为圆心的动圆与轴分别交于两点，延长分别交抛物线于两点；

①求直线的斜率；

②延长交轴于点，若，求的值.

Answer 1

【答案】(I) (II)①②

【解析】

(I)由抛物线的定义，可求出点的横坐标，代入方程中，求出点的纵坐标；

(II) ①设直线SA的斜率为k，可设出SA直线方程，与抛物线方程联立，求出点M的坐标，由题意可知：SA=SB，因此可求出直线SB的斜率，可设出直线SB的方程，同理，可以求出N点的坐标，代入斜率公式，求出直线的斜率；

②设出E点坐标，由，可得到，从而求出斜率k，求出A点坐标，同理求出B点坐标，利用余弦定理求出的值，也就求出的值。

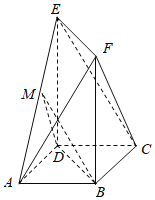
如下图所示：

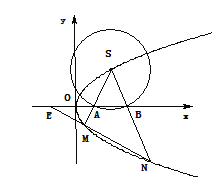
(I)设，抛物线的焦点为，准线方程为由抛物线的定义可知，所以点的坐标为（1，1）；

(II) ①设直线SA的直线方程为：与抛物线方程联立：

，设，，

所以，因为以为圆心的动圆与轴分别交于两点，所以SA=SB,因此直线SB的斜率为-k,同理可求出,；

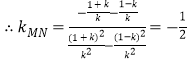②设， ,

，

则直线SA的方程为，A点坐标为，同理B点坐标为，,

，所以