Question

【题目】如图，在四棱锥中，底面是边长为2的正方形，平面 为等腰直角三角形，,为的中点，为的中点.

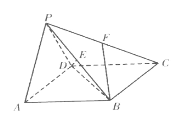
(1)求异面直线与所成角的余弦值；

(2)求二面角的余弦值.

Answer 1

【答案】（1）； （2）.

【解析】

（1）设AD的中点为G，根据面面垂直性质定理得平面ABCD，建立空间直角坐标系，设立各点坐标，利用向量数量积得夹角，即得结果，（2）利用方程组解得平面PBD的法向量，利用向量数量积得法向量夹角，最后根据二面角与向量夹角关系得结果.

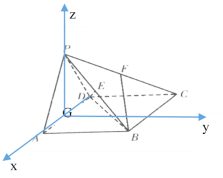
（1）如图，设AD的中点为G，连接PG，因为为等腰直角三角形，=90，所以.又平面平面ABCD,所以平面ABCD.

以G为坐标原点，GA,GP所在直线分别为x,z轴建立空间直角坐标系，

可得A（1,0,0），P（0,0,1）,B(1,2,0),C(-1,2,0),D(-1,0,0),则E（,1,）,F(-,1,),

所以,.故，

故异面直线ED与BF所成角的余弦值为.

（2）由（1）知，,设平面PBD的法向量为，

则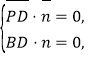 所以令

所以平面PBD的一个法向量为=(1,-1,-1).

易知平面ABD的一个法向量为=(0,0,1)，

所以，

由图可知，二面角A-BD-P为锐二面角，

所以二面角A-BD-P的余弦值为.