题目内容
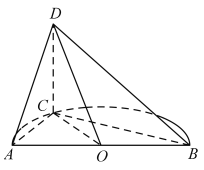
【题目】如图,在多面体ABCDEF中,ABCD是正方形,BF⊥平面ABCD,DE⊥平面ABCD,BF=DE,点M为棱AE的中点.
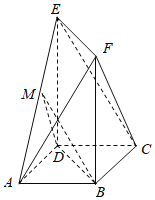
(1)求证:平面BMD∥平面EFC;
(2)若AB=1,BF=2,求三棱锥A-CEF的体积.
【答案】(1)见解析;
(2)![]() .
.
【解析】
(1)设AC与BD交于点N,则N为AC的中点,可得MN∥EC.由线面平行的判定,可得MN∥平面EFC.再由BF⊥平面ABCD,DE⊥平面ABCD,且BF=DE,可得BDEF为平行四边形,得到BD∥EF.由面面平行的判定,可得平面BDM∥平面EFC;
(2)连接EN,FN.在正方形ABCD中,AC⊥BD,再由BF⊥平面ABCD,可得BF⊥AC.从而得到AC⊥平面BDEF,然后代入棱锥体积公式求解.
(1)证明:设AC与BD交于点N,则N为AC的中点,而M为AE中点
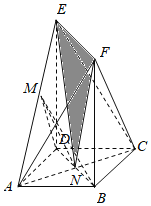
∴MN∥EC.
∵MN平面EFC,EC平面EFC,
∴MN∥平面EFC.
∵BF⊥平面ABCD,DE⊥平面ABCD,且BF=DE,
∴BF∥DE,BF=DE,
∴BDEF为平行四边形,∴BD∥EF.
∵BD平面EFC,EF平面EFC,
∴BD∥平面EFC.
又∵MN∩BD=N,
∴平面BDM∥平面EFC;
(2)解:连接EN,FN.在正方形ABCD中,AC⊥BD,
又∵BF⊥平面ABCD,∴BF⊥AC.
∵BF∩BD=B,
∴AC⊥平面BDEF,且垂足为N,
∴![]() ,
,
∴三棱锥A-CEF的体积为![]() .
.

 阅读快车系列答案
阅读快车系列答案【题目】天水市第一次联考后,某校对甲、乙两个文科班的数学考试成绩进行分析,
规定:大于或等于120分为优秀,120分以下为非优秀.统计成绩后,
得到如下的![]() 列联表,且已知在甲、乙两个文科班全部110人中随机抽取1人为优秀的概率为
列联表,且已知在甲、乙两个文科班全部110人中随机抽取1人为优秀的概率为![]() .
.
优秀 | 非优秀 | 合计 | |
甲班 | 10 | ||
乙班 | 30 | ||
合计 | 110 |
(1)请完成上面的列联表;
(2)根据列联表的数据,若按99.9%的可靠性要求,能否认为“成绩与班级有关系”;
(3)若按下面的方法从甲班优秀的学生中抽取一人:把甲班优秀的10名学生从2到11进行编号,先后两次抛掷一枚均匀的骰子,出现的点数之和为被抽取人的序号。试求抽到9号或10号的概率。
参考公式与临界值表:![]() 。
。
| 0.100 | 0.050 | 0.025 | 0.010 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
【题目】某互联网公司为了确定下一季度的前期广告投入计划,收集了近期前期广告投入量![]() (单位:万元)和收益
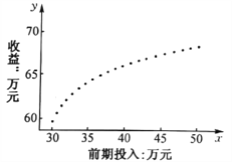
(单位:万元)和收益![]() (单位:万元)的数据。对这些数据作了初步处理,得到了下面的散点图(共
(单位:万元)的数据。对这些数据作了初步处理,得到了下面的散点图(共![]() 个数据点)及一些统计量的值.为了进一步了解广告投入量
个数据点)及一些统计量的值.为了进一步了解广告投入量![]() 对收益
对收益![]() 的影响,公司三位员工①②③对历史数据进行分析,查阅大量资料,分别提出了三个回归方程模型:
的影响,公司三位员工①②③对历史数据进行分析,查阅大量资料,分别提出了三个回归方程模型:
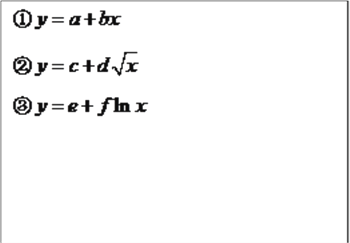
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
根据![]() ,
, ![]() ,参考数据:
,参考数据: ![]() ,
, ![]() .
.
(1)根据散点图判断,哪一位员工提出的模型不适合用来描述![]() 与
与![]() 之间的关系?简要说明理由.
之间的关系?简要说明理由.
(2)根据(1)的判断结果及表中数据,在余下两个模型中分别建立收益![]() 关于投入量
关于投入量![]() 的关系,并从数据相关性的角度考虑,在余下两位员工提出的回归模型中,哪一个是最优模型(即更适宜作为收益
的关系,并从数据相关性的角度考虑,在余下两位员工提出的回归模型中,哪一个是最优模型(即更适宜作为收益![]() 的回归方程)?说明理由;
的回归方程)?说明理由;
附:对于一组数据![]() ,
, ![]() ,…,
,…, ![]() ,其回归直线
,其回归直线![]() 的斜率、截距的最小二乘估计以及相关系数分别为:
的斜率、截距的最小二乘估计以及相关系数分别为:
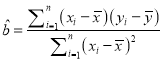 ,
, ![]() ,
, 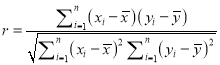 ,
,
其中![]() 越接近于
越接近于![]() ,说明变量
,说明变量![]() 与
与![]() 的线性相关程度越好.
的线性相关程度越好.