题目内容
【题目】已知销售“笔记本电脑”和“台式电脑”所得的利润分别是P（单位：万元）和Q（单位：万元），它们与进货资金t（单位：万元）的关系有经验公式P= 
t和Q= 
．某商场决定投入进货资金50万元，全部用来购入这两种电脑，那么该商场应如何分配进货资金，才能使销售电脑获得的利润y（单位：万元）最大？最大利润是多少万元？
【答案】解：设用于台式电脑的进货资金为m万元，则用于笔记本电脑的进货资金为（50﹣m）万元，脑获得的利润为y=P+Q= 
（50﹣m）+ 
（0≤m≤50）．
令u= ，则u∈[0，5 
]，
则y=﹣ u2+ u+ 
=﹣ （u﹣4）2+ 
．
当u=4，即m=16时，y取得最大值为 ．
所以当用于台式机的进货资金为16万元，用于笔记本的进货资金为34万元时，可使销售电脑的利润最大，最大为 万元
【解析】设用于台式电脑的进货资金为m万元，则用于笔记本电脑的进货资金为（50﹣m）万元，那么y=P+Q，代入可得关于x的解析式，利用换元法得到二次函数f（t），再由二次函数的图象与性质，可得结论．．
练习册系列答案
相关题目
【题目】某上市股票在30天内每股的交易价格P（元）与时间t（天）组成有序数对（t，P），点（t，P）落在下图中的两条线段上，该股票在30天内（包括30天）的日交易量Q（万股）与时间t（天）的部分数据如下表所示．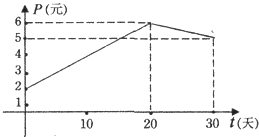 
第t天 | 4 | 10 | 16 | 22 |
Q（万股） | 36 | 30 | 24 | 18 |
（1）根据提供的图象，写出该种股票每股交易价格P（元）与时间t（天）所满足的函数关系式；
（2）根据表中数据确定日交易量Q（万股）与时间t（天）的一次函数关系式；
（3）在（2）的结论下，用y（万元）表示该股票日交易额，写出y关于t的函数关系式，并求出这30天中第几日交易额最大，最大值为多少？
