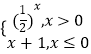题目内容
【题目】设数列{an}和{bn}的项数均为m,则将数列{an}和{bn}的距离定义为 ![]() |ai﹣bi|.
|ai﹣bi|.
(1)给出数列1,3,5,6和数列2,3,10,7的距离;
(2)设A为满足递推关系an+1= ![]() 的所有数列{an}的集合,{bn}和{cn}为A中的两个元素,且项数均为m,若b1=2,c1=3,{bn}和{cn}的距离小于2016,求m的最大值;
的所有数列{an}的集合,{bn}和{cn}为A中的两个元素,且项数均为m,若b1=2,c1=3,{bn}和{cn}的距离小于2016,求m的最大值;
(3)记S是所有7项数列{an|1≤n≤7,an=0或1}的集合,TS,且T中任何两个元素的距离大于或等于3,证明:T中的元素个数小于或等于16.
【答案】
(1)解:由题意可知,数列1,3,5,6和数列2,3,10,7的距离为1+0+5+1=7
(2)解:设a1=p,其中p≠0,且p≠±1,
由an+1= ![]() ,得a2=
,得a2= ![]() ,a3=﹣
,a3=﹣ ![]() ,a4=
,a4= ![]() ,a5=p,
,a5=p,
∴a1=a5,
因此A中数列的项周期性重复,且间隔4项重复一次,
所数列{bn}中,b4k﹣3=2,b4k﹣2=﹣3,b4k﹣1=﹣ ![]() ,b4k=
,b4k= ![]() ,k∈N*,
,k∈N*,
所以{cn}中,b4k﹣3=3,b4k﹣2=﹣2,b4k﹣1=﹣ ![]() ,b4k=
,b4k= ![]() ,k∈N*,
,k∈N*,
![]() |bi﹣ci|≥
|bi﹣ci|≥ ![]() |bi﹣ci|,得项数m越大,数列{bn}和{cn}的距离越大,
|bi﹣ci|,得项数m越大,数列{bn}和{cn}的距离越大,
由 ![]() =bi﹣ci|=
=bi﹣ci|= ![]() ,
,
得 ![]() |bi﹣ci|=
|bi﹣ci|= ![]() |bi﹣ci|=
|bi﹣ci|= ![]() ×864=2016,
×864=2016,
所以m<3456时, ![]() |bi﹣ci|<2016,
|bi﹣ci|<2016,
故m的最大值为3455
(3)解:证明:假设T中的元素个数大于等于17个,
因为数列{an}中,ai=0或1,
所以仅由数列前三项组成的数组(a1,a2,a3)有且仅有8个,(0,0,0),(1,0,0),(0,1,0),(0,0,1),(1,1,0),
(1,0,1),(0,1,1),(1,1,1),
那么这17个元素(即数列)之中必有三个具有相同的a1,a2,a3,
设这个数列分别为{cn}:c1,c2,c3,c4,c5,c6,c7,{dn}:d1,d2,d3,d4,d5,d6,d7,{fn}:f1,f2,f3,f4,f5,f6,f7,
其中c1=d1=f1,c2=d2=f2,c3=d3=f3,
因为这三个数列中每两个的距离大于等于3,
所以,{bn}和{cn}中,ci=di,(i=4,5,6,7)中至少有三个成立,
不妨设c4≠d4,c5≠d5,c6≠d6,
由题意,c4和d4中一个等于0,而另一个等于1,
又因为f4=0或1,
所以f4=c4和f4=d4中必有一个成立,
同理,得f5=c5和f5=d5中必有一个成立,f6=c6和f6=d6中必有一个成立,
所以“fi=ci(i=3,4,5)中至少有两个成立”或”fi=di(i=4,5,6)中至少有两个成立“中必有一个成立,
所以 ![]() |fi﹣ci|≤2和
|fi﹣ci|≤2和 ![]() |fi﹣di|≤2中必有一个成立.
|fi﹣di|≤2中必有一个成立.
与题意矛盾,
∴T中的元素个数小于或等于16
【解析】(1)由数列距离的定义即可求得数列1,3,5,6和数列2,3,10,7的距离;(2)由数列的递推公式,即可求得a,a3 , a4 , a5 , 求得A中数列的项周期性重复,且间隔4项重复一次,求得数列{bn}和{cn}规律,可知随着项数m越大,数列{bn}和{cn}的距离越大,由 ![]() =bi﹣ci|=
=bi﹣ci|= ![]() ,根据周期的定义,得
,根据周期的定义,得 ![]() |bi﹣ci|=
|bi﹣ci|= ![]() |bi﹣ci|=
|bi﹣ci|= ![]() ×864=2016,求得m的最大值;(3)利用反证法,假设T中的元素个数大于等于17个,设出{cn},{dn},{fn},最总求得
×864=2016,求得m的最大值;(3)利用反证法,假设T中的元素个数大于等于17个,设出{cn},{dn},{fn},最总求得 ![]() |fi﹣ci|≤2和
|fi﹣ci|≤2和 ![]() |fi﹣di|≤2中必有一个成立,与数列的距离大于或等于3矛盾,故可证明T中的元素个数小于或等于16.
|fi﹣di|≤2中必有一个成立,与数列的距离大于或等于3矛盾,故可证明T中的元素个数小于或等于16.