题目内容
(本小题满分12分,(Ⅰ)小问6分,(Ⅱ)小问6分.)
如图(20)图,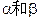 为平面,
为平面,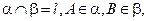 AB=5,A,B在棱l上的射影分别为A′,B′,AA′=3,BB′=2.若二面角
AB=5,A,B在棱l上的射影分别为A′,B′,AA′=3,BB′=2.若二面角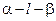 的大小为
的大小为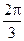 ,求:
,求:
(Ⅰ)点B到平面 的距离;
的距离;
(Ⅱ)异面直线l与AB所成的角(用反三角函数表示).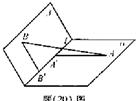
如图(20)图,
 为平面,
为平面, AB=5,A,B在棱l上的射影分别为A′,B′,AA′=3,BB′=2.若二面角
AB=5,A,B在棱l上的射影分别为A′,B′,AA′=3,BB′=2.若二面角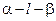 的大小为
的大小为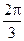 ,求:
,求:(Ⅰ)点B到平面
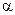 的距离;
的距离;(Ⅱ)异面直线l与AB所成的角(用反三角函数表示).

(Ⅰ)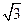
(Ⅱ)arcsin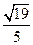
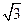
(Ⅱ)arcsin
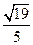
本题主要考查立体几何中的主干知识,如线线角、二面角等基础知识,考查空间想象能力、逻辑思维能力和运算能力。解题的关键是线面平行、三垂线定理等基础知识,本题属中等题。
(1)过点B′作直线B′C∥A′A且使B′C=A′A.过点B作BD⊥CB′,交CB′的延长线于D.
由已知AA′⊥l,可得DB′⊥l,又已知BB′⊥l,故l⊥平面BB′D,得BD⊥l又因BD⊥CB′,从而BD⊥平面α,BD之长即为点B到平面α的距离.
因B′C⊥l且BB′⊥l,故∠BB′C为二面角α-l-β的平面角.由题意,∠BB′C=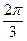 .因此在Rt△BB′D中,BB′=2,∠BB′D=π-∠BB′C=
.因此在Rt△BB′D中,BB′=2,∠BB′D=π-∠BB′C=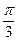 ,BD=BB′·sinBB′D=
,BD=BB′·sinBB′D=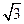 .
.
(Ⅱ)连接AC、BC.因B′C∥A′A,B′C=A′A,AA′⊥l,知A′ACB′为矩形,故AC∥l.所以∠BAC或其补角为异面直线l与AB所成的角.
在△BB′C中,B′B=2,B′C=3,∠BB′C=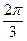 ,则由余弦定理,
,则由余弦定理,
BC=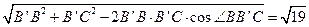 .
.
因BD 平面
平面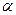 ,且DC
,且DC CA,由三垂线定理知AC
CA,由三垂线定理知AC BC.
BC.
故在△ABC中,∠BCA=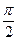 ,sinBAC=
,sinBAC=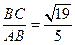 .
.
因此,异面直线l与AB所成的角为arcsin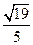
(1)过点B′作直线B′C∥A′A且使B′C=A′A.过点B作BD⊥CB′,交CB′的延长线于D.
由已知AA′⊥l,可得DB′⊥l,又已知BB′⊥l,故l⊥平面BB′D,得BD⊥l又因BD⊥CB′,从而BD⊥平面α,BD之长即为点B到平面α的距离.
因B′C⊥l且BB′⊥l,故∠BB′C为二面角α-l-β的平面角.由题意,∠BB′C=
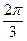 .因此在Rt△BB′D中,BB′=2,∠BB′D=π-∠BB′C=
.因此在Rt△BB′D中,BB′=2,∠BB′D=π-∠BB′C=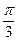 ,BD=BB′·sinBB′D=
,BD=BB′·sinBB′D=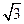 .
.(Ⅱ)连接AC、BC.因B′C∥A′A,B′C=A′A,AA′⊥l,知A′ACB′为矩形,故AC∥l.所以∠BAC或其补角为异面直线l与AB所成的角.
在△BB′C中,B′B=2,B′C=3,∠BB′C=
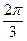 ,则由余弦定理,
,则由余弦定理,BC=
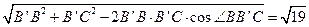 .
.因BD
 平面
平面 ,且DC
,且DC CA,由三垂线定理知AC
CA,由三垂线定理知AC BC.
BC.故在△ABC中,∠BCA=
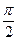 ,sinBAC=
,sinBAC=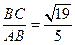 .
.因此,异面直线l与AB所成的角为arcsin
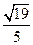

练习册系列答案
 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案
相关题目
 中,AP=BQ=b(0<b<1),截面PQEF∥
中,AP=BQ=b(0<b<1),截面PQEF∥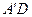 ,截面PQGH∥
,截面PQGH∥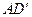 .
.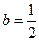 ,求
,求 与平面PQEF所成角的正弦值.
与平面PQEF所成角的正弦值.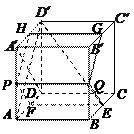


 内作菱形ABCD,边长为1,∠BAD=60°,再在
内作菱形ABCD,边长为1,∠BAD=60°,再在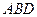 与△
与△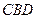 为底面安装上相同的正棱锥P-ABD与Q-CBD,∠APB=90°.
为底面安装上相同的正棱锥P-ABD与Q-CBD,∠APB=90°.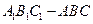 中,
中,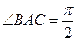 ,
,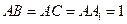 . 已知G与E分别为
. 已知G与E分别为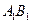 和
和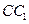 的中点,D与F分别为线段
的中点,D与F分别为线段 和
和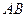 上的动点(不包括端点). 若
上的动点(不包括端点). 若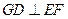 ,则线段
,则线段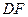 的长度的取值范围为
的长度的取值范围为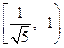



 的各顶点都在球
的各顶点都在球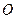 的球面上,其中
的球面上,其中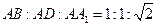 .
.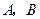 两点的球面距离记为
两点的球面距离记为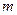 ,
,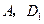 两点的球面距离记为
两点的球面距离记为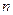 ,则
,则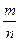 的值为 .
的值为 .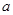 升水时,水面恰好经过正四棱锥的顶点P。如果将容器倒置,水面也恰好过点
升水时,水面恰好经过正四棱锥的顶点P。如果将容器倒置,水面也恰好过点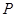 (图2)。有下列四个命题:
(图2)。有下列四个命题: