题目内容
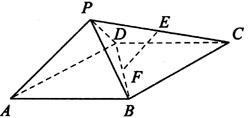
图4,四棱锥P—ABCD中,ABCD为矩形,△PAD为等腰直角三角形,

∠APD=90°,面PAD⊥面ABCD,且AB=1,AD=2,E、F分别为PC和BD的中点.
(1)证明:EF∥面PAD;
(2)证明:面PDC⊥面PAD.

∠APD=90°,面PAD⊥面ABCD,且AB=1,AD=2,E、F分别为PC和BD的中点.
(1)证明:EF∥面PAD;
(2)证明:面PDC⊥面PAD.
 |
(1)(2)见解析
(1)如图,连接AC,
∵ABCD为矩形且F是BD的中点,
∴AC必经过F 。
又E是PC的中点,
所以,EF∥AP。
∵EF在面PAD外,PA在面内,
∴EF∥面PAD
(2)∵面PAD⊥面ABCD,CD⊥AD,面PAD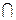 面ABCD=AD,
面ABCD=AD,
∴CD⊥面PAD, 8分
又AP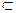 面PAD,∴AP⊥CD. 9分
面PAD,∴AP⊥CD. 9分
又∵AP⊥PD,PD和CD是相交直线,AP⊥面PCD。
又AD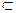 面PAD,所以,面PDC⊥面PAD 。
面PAD,所以,面PDC⊥面PAD 。

∵ABCD为矩形且F是BD的中点,
∴AC必经过F 。
又E是PC的中点,
所以,EF∥AP。
∵EF在面PAD外,PA在面内,
∴EF∥面PAD
(2)∵面PAD⊥面ABCD,CD⊥AD,面PAD
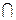 面ABCD=AD,
面ABCD=AD,∴CD⊥面PAD, 8分
又AP
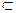 面PAD,∴AP⊥CD. 9分
面PAD,∴AP⊥CD. 9分又∵AP⊥PD,PD和CD是相交直线,AP⊥面PCD。
又AD
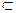 面PAD,所以,面PDC⊥面PAD 。
面PAD,所以,面PDC⊥面PAD 。
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
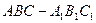 中,
中,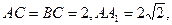 ∠ACB=90°,M是
∠ACB=90°,M是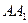 的中点,N是
的中点,N是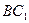 的中点。
的中点。 ;
;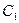 到平面BMC的距离;
到平面BMC的距离;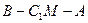 1的大小。
1的大小。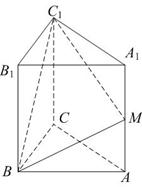
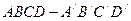 中
中
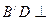 平面
平面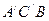 ;
;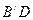 与平面
与平面 是
是 的重心(三角形三条中线的交点)
的重心(三角形三条中线的交点)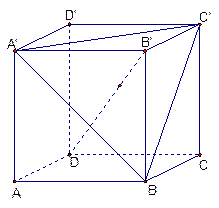
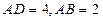 ,E、F分别是线段AB、BC的中点,
,E、F分别是线段AB、BC的中点,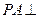 面ABCD. (1)
面ABCD. (1)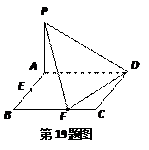 证明:PF⊥FD;
证明:PF⊥FD;
 和矩形
和矩形 所在的平面互相垂直,
所在的平面互相垂直, ,
,
 是线段
是线段 的中点.
的中点.
 ;(2)求二面角
;(2)求二面角 的大小;
的大小;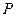 为一动点,若点
为一动点,若点
 ,求这一过程中形成的三棱锥
,求这一过程中形成的三棱锥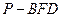 的体积的最小值.
的体积的最小值.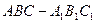 中,
中,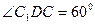 .
.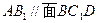 (5分)
(5分)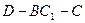 的大小。(7分)
的大小。(7分)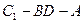 平面角的大小。(7分)
平面角的大小。(7分)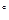 ,在四边形ABCD中,∠ADC=∠DAB=90
,在四边形ABCD中,∠ADC=∠DAB=90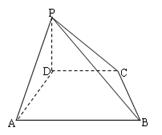
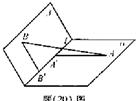
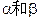 为平面,
为平面,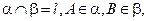 AB=5,A,B在棱l上的射影分别为A′,B′,AA′=3,BB′=2.若二面角
AB=5,A,B在棱l上的射影分别为A′,B′,AA′=3,BB′=2.若二面角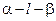 的大小为
的大小为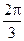 ,求:
,求: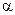 的距离;
的距离;