��Ŀ����
����Ŀ����ijУ�����ȡ�������������������ʲ��ԣ������ʵ����ijɼ����ݣ������õ����ݷ��鼰Ƶ�ʷֲ������ɼ���11.0�ף���ȷ��0.1�ף����ϣ�����������Ϊ������������
���飨�ף� | Ƶ�� | Ƶ�� |
[3.0��5.0�� | 0.10 | |
[5.0��7.0�� | 0.10 | |
[7.0��9.0�� | 0.10 | |
[9.0��11.0�� | 0.20 | |
[11.0��13.0�� | 0.40 | |
[13.0��15.0�� | 10 | |
�ϼ� | 1.00 |
������μӲ��Ե������С�����������������
���ӲμӲ��������ijɼ��У����ݱ��з�����������ֲ�����ķ�����ȡ10�������ijɼ���Ϊһ���������ٴӸ���������ѡ2�������ijɼ���������ѡ��1�������ijɼ�������13.0�ĸ��ʣ�
����������β��Ե�Ƶ����Ϊ���ʣ��Ӹ�Уȫ�������������ȡ3�ˣ���X��ʾ3���С�������������������X�ķֲ��м���ѧ������
���𰸡��⣺����6С���Ƶ��Ϊ1����0.10+0.10+0.20+0.40��=0.10��
�ߵ�6С���Ƶ��Ϊ10����������Ϊ ![]() =100���ˣ���
=100���ˣ���
���5��6���ѧ����Ϊ����������������Ϊ��0.40+0.10����100=50���ˣ���
������������������Ϊ50�� ��
���� ���ݷֲ�������ڸ����ȡ�������ֱ�1�ˣ�1�ˣ�1�ˣ�2�ˣ�4�ˣ�1�ˣ����гɼ�������13.0����1�ˣ�
���¼�AΪ������1�������ɼ�������13.0�ס�����P��A��= ![]() =
= ![]() ��
��
��ѡ����2�������ijɼ���������1�������ijɼ�������13.0�ĸ���Ϊ ![]() ����
����
���Ӹ�Уȫ����������ѡһ�ˣ�������ǡ����������ĸ���Ϊ ![]() ��
��
������֪X�Ŀ���ȡֵΪ0��1��2��3��
P��X=0��= ![]() ��
��
P��X=1��= ![]() ��
��
P��X=2��= ![]() =
= ![]() ��
��
P��X=3��= ![]() =
= ![]() ��
��
����ֲ���Ϊ��
X | 0 | 1 | 2 | 3 |
P |
|
|
|
|
��EX= ![]() =
= ![]() ����
����
��������1��������ɵõ�6С���Ƶ��Ϊ1����0.10+0.10+0.20+0.40��=0.10����5��6���ѧ����Ϊ����������������Ϊ��0.40+0.10����100=50���ˣ���������������������Ϊ50�� ��
2�����⿼�����"����"�ĸ�������
���¼�AΪ������1�������ɼ�������13.0�ס�����P��A��= ![]() =
= ![]() ����ѡ����2�������ijɼ���������1�������ijɼ�������13.0�ĸ���Ϊ
����ѡ����2�������ijɼ���������1�������ijɼ�������13.0�ĸ���Ϊ ![]()
3��������֪X�Ŀ���ȡֵΪ0��1��2��3��
P��X=0��= ![]() ��
��
P��X=1��= ![]() ��
��
P��X=2��= ![]() =
= ![]() ��
��
P��X=3��= ![]() =
= ![]() ��
��
�б��ɵ�X�ķֲ��У�����ֵ�ɹ�ʽ�ɵá�
�����㾫����������Ҫ��������ɢ�������������ֲ��е����֪ʶ�㣬��Ҫ�������������Ʒ����������У������������X����ȡ��ֵ�����ǿ���һ������һһ�г����������������������ɢ�������������ɢ����������ķֲ��У�һ���,����ɢ���������X����ȡ��ֵΪx1,x2,.....,xi,......,xn��Xȡÿһ��ֵ xi(i=1,2,......���ĸ���P(��=xi����Pi����Ʊ�Ϊ��ɢ���������X �ĸ��ʷֲ�����Ʒֲ��в�����ȷ�����⣮

����Ŀ�������ƶ��������Ŀ��ٷ�չ�����ڻ������Ĺ�������Ӧ�˶�����ij�г��о���ԱΪ���˽��������Ӫ��˾M�ľ�Ӫ״�����Ըù�˾����������ڵ��г�ռ���ʽ�����ͳ�ƣ�����������Ӧ������ͼ��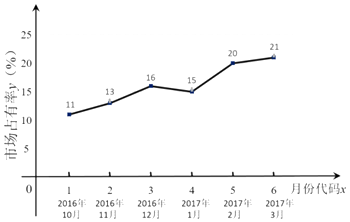
����������ͼ���Կ������������Իع�ģ������¶��г�ռ����y���·ݴ���x֮��Ĺ�ϵ����y����x�����Իع鷽�̣���Ԥ��M��˾2017��4�·ݵ��г�ռ���ʣ�
����Ϊ��һ�������г�����˾���ٲɹ�һ�����������вɹ��ɱ��ֱ�Ϊ1000Ԫ/����1200Ԫ/����A��B����Ϳɹ�ѡ���涨ÿ���������ʹ��4�꣬�����ڶ���ԭ��������Ƶ�ʵȣ��ᵼ�³���������������ͬ�����ǵ���˾��Ӫ�ľ���Ч�棬�ù�˾�����ȶ�����͵ĵ�����100�����п�ѧģ����ԣ��õ������ʹ������Ƶ�������£�
�������� | 1�� | 2�� | 3�� | 4�� | �ܼ� |
A | 20 | 35 | 35 | 10 | 100 |
B | 10 | 30 | 40 | 20 | 100 |
�����㣬ƽ��ÿ������ÿ����Դ�������500Ԫ�������dz��ɹ��ɱ�֮��������ɱ�������ÿ��������ʹ���������������꣬����Ƶ����Ϊÿ������ʹ�������ĸ��ʣ��������M��˾�ĸ����ˣ���ÿ�������������������ֵΪ�������ݣ����ѡ��ɹ��Ŀ�ͣ�
�ο����ݣ��� ![]() ��
�� ![]() =17.5��
=17.5��
�ο���ʽ��
�ع�ֱ�߷���Ϊ ![]() ����
���� ![]() =
= 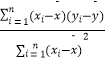 ��
�� ![]() =
= ![]() ��
�� ![]() ��
��
