题目内容
【题目】随着移动互联网的快速发展,基于互联网的共享单车应运而生.某市场研究人员为了了解共享单车运营公司M的经营状况,对该公司最近六个月内的市场占有率进行了统计,并绘制了相应的折线图.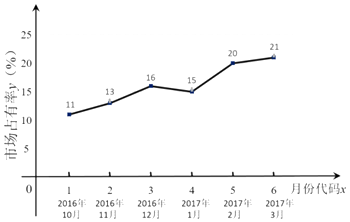
(Ⅰ)由折线图可以看出,可用线性回归模型拟合月度市场占有率y与月份代码x之间的关系.求y关于x的线性回归方程,并预测M公司2017年4月份的市场占有率;
(Ⅱ)为进一步扩大市场,公司拟再采购一批单车.现有采购成本分别为1000元/辆和1200元/辆的A、B两款车型可供选择,按规定每辆单车最多使用4年,但由于多种原因(如骑行频率等)会导致车辆报废年限各不相同.考虑到公司运营的经济效益,该公司决定先对两款车型的单车各100辆进行科学模拟测试,得到两款单车使用寿命频数表如下:
报废年限 | 1年 | 2年 | 3年 | 4年 | 总计 |
A | 20 | 35 | 35 | 10 | 100 |
B | 10 | 30 | 40 | 20 | 100 |
经测算,平均每辆单车每年可以带来收入500元.不考虑除采购成本之外的其他成本,假设每辆单车的使用寿命都是整数年,且以频率作为每辆单车使用寿命的概率.如果你是M公司的负责人,以每辆单车产生利润的期望值为决策依据,你会选择采购哪款车型?
参考数据:, ![]() ,
, ![]() =17.5.
=17.5.
参考公式:
回归直线方程为 ![]() 其中
其中 ![]() =
= 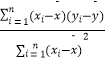 ,
, ![]() =
= ![]() ﹣
﹣ ![]() .
.
【答案】解:(Ⅰ)由题意, ![]() =3.5,
=3.5, ![]() =16,
=16, ![]() =
= ![]() =2,
=2, ![]() =
= ![]() ﹣
﹣ ![]()
![]() =16﹣2×3.5=9,
=16﹣2×3.5=9,
∴ ![]() =2x+9,
=2x+9,
x=7时, ![]() =2×7+9=23,即预测M公司2017年4月份(即x=7时)的市场占有率为23%;
=2×7+9=23,即预测M公司2017年4月份(即x=7时)的市场占有率为23%;
(Ⅱ)由频率估计概率,每辆A款车可使用1年,2年,3年、4年的概率分别为0.2,0.35,0.35,0.1,
∴每辆A款车的利润数学期望为(500﹣1000)×0.2+(1000﹣1000)×0.35+(1500﹣1000)×0.35+(2000﹣1000)×0.1=175元;
每辆B款车可使用1年,2年,3年、4年的概率分别为0.1,0.3,0.4,0.2,
∴每辆B款车的利润数学期望为(500﹣1200)×0.1+(1000﹣1200)×0.3+(1500﹣1200)×0.4+(2000﹣1200)×0.2=150元;
∵175>150,
∴应该采购A款车.
【解析】1、由折线图可以看出,可用线性回归模型拟合月度市场占有率y与月份代码x之间的关系,即预测M公司2017年4月份(即x=7时)的市场占有率为23%;
2、由频率估计概率,每辆A款车可使用1年,2年,3年、4年的概率分别为0.2,0.35,0.35,0.1,
∴每辆A款车的利润数学期望为(500﹣1000)×0.2+(1000﹣1000)×0.35+(1500﹣1000)×0.35+(2000﹣1000)×0.1=175元;
每辆B款车可使用1年,2年,3年、4年的概率分别为0.1,0.3,0.4,0.2,
∴每辆B款车的利润数学期望为(500﹣1200)×0.1+(1000﹣1200)×0.3+(1500﹣1200)×0.4+(2000﹣1200)×0.2=150元;
∵175>150,∴应该采购A款车.

【题目】命题p:数列{an}的前n项和Sn=an2+bn+c(a≠0);命题q:数列{an}是等差数列.则p是q的( )
A.充分而不必要条件
B.必要而不充分条件
C.充分必要条件
D.既不充分也不必要条件
【题目】从某校随机抽取部分男生进行身体素质测试,获得掷实心球的成绩数据,整理得到数据分组及频率分布表,成绩在11.0米(精确到0.1米)以上(含)的男生为“优秀生”.
分组(米) | 频数 | 频率 |
[3.0,5.0) | 0.10 | |
[5.0,7.0) | 0.10 | |
[7.0,9.0) | 0.10 | |
[9.0,11.0) | 0.20 | |
[11.0,13.0) | 0.40 | |
[13.0,15.0) | 10 | |
合计 | 1.00 |
(Ⅰ)求参加测试的男生中“优秀生”的人数;
(Ⅱ)从参加测试男生的成绩中,根据表中分组情况,按分层抽样的方法抽取10名男生的成绩作为一个样本,再从该样本中任选2名男生的成绩,求至少选出1名男生的成绩不低于13.0米的概率;
(Ⅲ)若将这次测试的频率作为概率,从该校全体男生中随机抽取3人,记X表示3人中“优秀生”的人数,求X的分布列及数学期望.