题目内容
已知圆C的圆心在直线3x-y=0上且在第一象限,圆C与x轴相切,且被直线x-y=0截得的弦长为2
.
(1)求圆C的方程;
(2)若点P(x,y)是圆C上的点,满足
x+y-m≤0恒成立,求m的取值范围;
(3)将圆C向左移1个单位,再向下平移3个单位得到圆C1,P为圆C1上第一象限内的任意一点,过点P作圆C1的切线l,且l交x轴于点A,交y轴于点B,设
=
+
,求丨
丨的最小值(O为坐标原点).
| 7 |
(1)求圆C的方程;
(2)若点P(x,y)是圆C上的点,满足
| 3 |
(3)将圆C向左移1个单位,再向下平移3个单位得到圆C1,P为圆C1上第一象限内的任意一点,过点P作圆C1的切线l,且l交x轴于点A,交y轴于点B,设
| OM |
| OA |
| OB |
| OM |
(1)根据题意设圆心C(a,3a),a>0,半径为3a,
∵圆心到直线x-y=0的距离d=
=2a,弦长为2
,半径为3a,
∴2
=2
,即7a2=7,
解得:a=1,则圆C方程为(x-1)2+(y-3)2=9.
(2)根据圆C方程设x=1+cosα,y=3+sinα,
不等式
x+y-m≤0恒成立,即为m≥
x+y恒成立,
∵
x+y=
+3+
cosα+sinα=
+3+2sin(α+θ)的最大值为
+3+2=
+5,
则m满足m≥
+5,故 m的取值范围为[
+5,+∞).
(3)由条件利用平移规律确定出圆C1的方程为 (x-0)2+(y-0)2=9,
设点P的坐标为(x0,y0),则有x0>0,y0>0,且x02+y02=9,
故切线l的方程为 x0•x+y0•y=9,
由此可得点A(
,0),点B的坐标为(0,
),
∴
=
+
=(
,
),
∵圆心到直线x-y=0的距离d=
| |a-3a| |
| 2 |
| 7 |
∴2
| 7 |
| r2-d2 |
解得:a=1,则圆C方程为(x-1)2+(y-3)2=9.
(2)根据圆C方程设x=1+cosα,y=3+sinα,
不等式
| 3 |
| 3 |
∵
| 3 |
| 3 |
| 3 |
| 3 |
| 3 |
| 3 |
则m满足m≥
| 3 |
| 3 |
(3)由条件利用平移规律确定出圆C1的方程为 (x-0)2+(y-0)2=9,
设点P的坐标为(x0,y0),则有x0>0,y0>0,且x02+y02=9,
故切线l的方程为 x0•x+y0•y=9,
由此可得点A(
| 9 |
| x0 |
| 9 |
| y0 |
∴
| OM |
| OA |
| OB |
| 9 |
| x0 |
| 9 |
| y0 |

练习册系列答案
 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案
相关题目
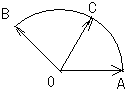
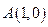 ,直线
,直线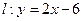 ,点
,点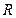 是直线
是直线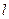 上的一点,若
上的一点,若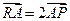 ,求点
,求点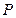 的轨迹方程.
的轨迹方程.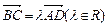 ,
,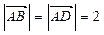 ,
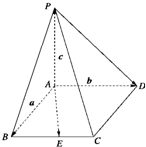
,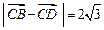 .⑴若△BCD是直角三形,求
.⑴若△BCD是直角三形,求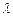 的值;⑵在⑴的条件下,求
的值;⑵在⑴的条件下,求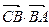 .
.
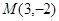 ,
,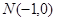 ,则线段
,则线段 的中点
的中点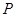 的坐标是________.
的坐标是________. (
(


 ),其左焦点
),其左焦点 与点P(1,
与点P(1, )的连线与圆
)的连线与圆 相切。
相切。 为直径的圆与圆
为直径的圆与圆 的位置关系,并证明
的位置关系,并证明