题目内容
(本小题满分12分)在四边形ABCD中, BD是它的一条对角线,且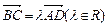 ,
,
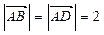 ,
,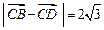 .⑴若△BCD是直角三形,求
.⑴若△BCD是直角三形,求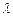 的值;⑵在⑴的条件下,求
的值;⑵在⑴的条件下,求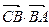 .
.
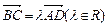 ,
,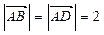 ,
,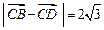 .⑴若△BCD是直角三形,求
.⑴若△BCD是直角三形,求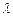 的值;⑵在⑴的条件下,求
的值;⑵在⑴的条件下,求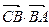 .
.(Ⅰ)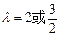 (Ⅱ)-3
(Ⅱ)-3
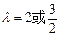 (Ⅱ)-3
(Ⅱ)-3(Ⅰ)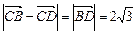 ,在
,在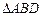 中,由余弦定理,得
中,由余弦定理,得 ,∴
,∴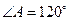 ,(2分)由
,(2分)由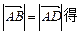 ,
,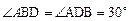 , 由
, 由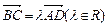 得,
得,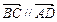 ,
,
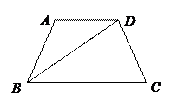
∴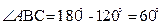 ,从而
,从而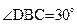 (4分)
(4分)
由题意可知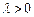 ,∴
,∴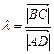 , (5分)
, (5分)
又∵△BCD是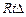 ,∴
,∴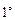 当
当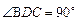 时,则
时,则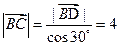 ,由
,由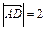 ,
,
∴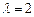 ;
;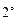 当
当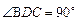 时,则
时,则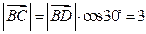 ,由
,由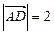 ,∴
,∴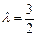 ;
;
综上,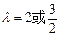 .(7分)
.(7分)
(Ⅱ)由(1)知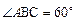 ,∴向量
,∴向量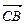 与
与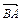 的夹角为
的夹角为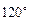 ,
,  (9分)
(9分)
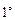 当
当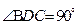 时,
时, ,
,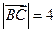 ,
,
∴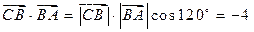 .
. (10分)
(10分)
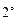 当
当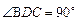 时,
时, ,
,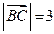 ,
,
∴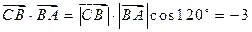 .
.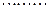 (12分)
(12分)
评析:本题考查平面向量和解三角形的基础知识,考查分类讨论的思想方法.求解时容易发生的错误是:(1)将条件“△BCD是直角三形”当作“△BCD是以角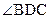 是直角三形”来解,忽略对
是直角三形”来解,忽略对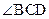 为直角的情况的讨论;(2)在计算
为直角的情况的讨论;(2)在计算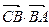 时,将
时,将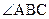 当作向量
当作向量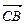 与
与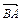 的夹角,忽略了确定两个向量的夹角时必须将它们的起点移到一起.暴露出思维的不严谨和概念理解的缺陷,在复习中要引起重视,加强训练.
的夹角,忽略了确定两个向量的夹角时必须将它们的起点移到一起.暴露出思维的不严谨和概念理解的缺陷,在复习中要引起重视,加强训练.
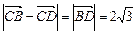 ,在
,在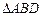 中,由余弦定理,得
中,由余弦定理,得 ,∴
,∴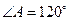 ,(2分)由
,(2分)由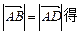 ,
,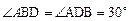 , 由
, 由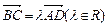 得,
得,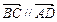 ,
,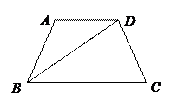
∴
 ,从而
,从而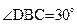 (4分)
(4分)由题意可知
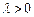 ,∴
,∴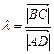 , (5分)
, (5分)又∵△BCD是
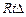 ,∴
,∴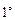 当
当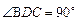 时,则
时,则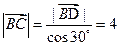 ,由
,由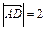 ,
,∴
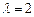 ;
;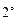 当
当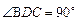 时,则
时,则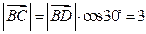 ,由
,由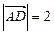 ,∴
,∴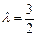 ;
;综上,
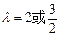 .(7分)
.(7分)(Ⅱ)由(1)知
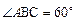 ,∴向量
,∴向量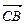 与
与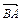 的夹角为
的夹角为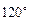 ,
, 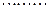 (9分)
(9分)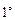 当
当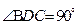 时,
时, ,
,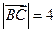 ,
,∴
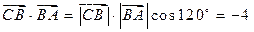 .
. (10分)
(10分) 当
当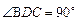 时,
时, ,
,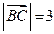 ,
,∴
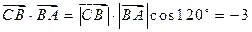 .
. (12分)
(12分)评析:本题考查平面向量和解三角形的基础知识,考查分类讨论的思想方法.求解时容易发生的错误是:(1)将条件“△BCD是直角三形”当作“△BCD是以角
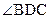 是直角三形”来解,忽略对
是直角三形”来解,忽略对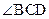 为直角的情况的讨论;(2)在计算
为直角的情况的讨论;(2)在计算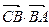 时,将
时,将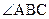 当作向量
当作向量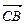 与
与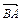 的夹角,忽略了确定两个向量的夹角时必须将它们的起点移到一起.暴露出思维的不严谨和概念理解的缺陷,在复习中要引起重视,加强训练.
的夹角,忽略了确定两个向量的夹角时必须将它们的起点移到一起.暴露出思维的不严谨和概念理解的缺陷,在复习中要引起重视,加强训练.
练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目



 ,
, ,
, .是否存在实数
.是否存在实数 ,使得
,使得 .若存在,求出
.若存在,求出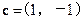 ,b·c=4,则b=____________.
,b·c=4,则b=____________. 是等腰梯形,
是等腰梯形, 、
、 分别是腰
分别是腰 、
、 的中点,
的中点, 、
、 是线段
是线段 上的两个点,且
上的两个点,且 ,下底是上底的2倍,若
,下底是上底的2倍,若 ,
, ,求
,求 .
.

 分别是双曲线
分别是双曲线 的左、右焦点,过
的左、右焦点,过 斜率为
斜率为 的直线
的直线 交双曲线的左、右两支分别于
交双曲线的左、右两支分别于 两点,过
两点,过 且与
且与 交双曲线的左、右两支分别于
交双曲线的左、右两支分别于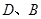 两点。
两点。 面积的最小值。
面积的最小值。