题目内容
已知四棱锥P-ABCD中,底面ABCD为菱形,∠ABC=60°,PA⊥平面ABCD,E为BC中点,求证:AE⊥PD.
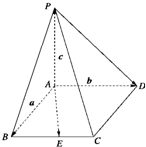

证:设
=
,
=
,
=
,
∵PA⊥平面ABCD,
∴
•
=0,
•
=0,
∵∠ABC=60°,四边形ABCD为菱形,
∴
•
=|
|•|
|•cos∠BAD=|
|2•cos120°
=-
|
|2.
=
+
=
+
,
=
+
+
+
=-
+
+
-
=
-
,
•
=(
+
)•(
-
)
=
•
+
|
|2-
•
-
•
=-
|
|2+
|
|2=0,
∴
⊥
,
∴AE⊥PD.
| AB |
| a |
| AD |
| b |
| AP |
| c |
∵PA⊥平面ABCD,
∴
| a |
| c |
| b |
| c |
∵∠ABC=60°,四边形ABCD为菱形,
∴
| a |
| b |
| a |
| b |
| b |
=-
| 1 |
| 2 |
| b |
| AE |
| AB |
| BE |
| a |
| 1 |
| 2 |
| b |
| PD |
| PA |
| AB |
| BC |
| CD |
| c |
| a |
| b |
| a |
| b |
| c |
| AE |
| PD |
| a |
| 1 |
| 2 |
| b |
| b |
| c |
=
| a |
| b |
| 1 |
| 2 |
| b |
| a |
| c |
| 1 |
| 2 |
| b |
| c |
=-
| 1 |
| 2 |
| b |
| 1 |
| 2 |
| b |
∴
| AE |
| PD |
∴AE⊥PD.

练习册系列答案
相关题目
 ,
, ,
, .是否存在实数
.是否存在实数 ,使得
,使得 .若存在,求出
.若存在,求出 上一点M到左焦点
上一点M到左焦点 的距离为2,N是
的距离为2,N是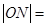 ( )
( ) 值;
值; 的值
的值