题目内容
已知向量a=（cosα，sinα），b=（cosβ，sinβ），且a，b满足|ka+b|=
|a-kb|（k＞0），
（1）求a与b的数量积用k表示的解析式f（k）；
（2）a能否和b垂直？a能否和b平行？若不能，请说明理由；若能，请求出相应的k值；
（3）求向量a与向量b的夹角的最大值．
| 3 |
（1）求a与b的数量积用k表示的解析式f（k）；
（2）a能否和b垂直？a能否和b平行？若不能，请说明理由；若能，请求出相应的k值；
（3）求向量a与向量b的夹角的最大值．
（1）由题，|
|=|
|=1且|k
+
|=
|
-k
|，
所以(k
+
)2=3(
-k
)2，
化简可得4k
•
=k2+1，
∴f(k)=
•
=
(k＞0)；
（2）若
⊥
，则
•
=
=0，而
=0无解，因此
和
不可能垂直；
若
∥
，则|
•
|=|
||
|即
=1，解得k=2±
，
综上，
和
不可能垂直；
当
和
平行时，k=2±
；
（3）设
与
夹角为θ，
则cosθ=
=
=
+
=(
)2+(
)2
=(
-
)2+
≥
因此，当且仅当
=
即k=1时，cosθ有最小值为
，此时，向量
与
的夹角有最大值为60°．
| a |
| b |
| a |
| b |
| 3 |
| a |
| b |
所以(k
| a |
| b |
| a |
| b |
化简可得4k
| a |
| b |
∴f(k)=
| a |
| b |
| k2+1 |
| 4k |
（2）若
| a |
| b |
| a |
| b |
| k2+1 |
| 4k |
| k2+1 |
| 4k |
| a |
| b |
若
| a |
| b |
| a |
| b |
| a |
| b |
| k2+1 |
| 4k |
| 3 |
综上，
| a |
| b |
当
| a |
| b |
| 3 |
（3）设
| a |
| b |
则cosθ=
| ||||
|
|
| k2+1 |
| 4k |
| k |
| 4 |
| 1 |
| 4k |
| ||
| 2 |
| 1 | ||
2
|
=(
| ||
| 2 |
| 1 | ||
2
|
| 1 |
| 2 |
| 1 |
| 2 |
因此，当且仅当
| ||
| 2 |
| 1 | ||
2
|
| 1 |
| 2 |
| a |
| b |
练习册系列答案
励耘书业暑假衔接宁波出版社系列答案
相关题目
的实轴长是（ ）
，
），且与直线l:y=
相切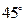 
，求Q点横坐标.