题目内容
【题目】已知三角形ABC的三边长为a、b、c，且其中任意两边长均不相等.若
，
，
成等差数列.（1）比较
与
的大小，并证明你的结论；（2）求证B不可能是钝角
【答案】见解析.
【解析】（1）此题可以先采用特值验证出结论，然后再利用分析法进行证明.
（2）本题易采用反证法.然后利用余弦定理结合基本不等式，推出矛盾从而达到证明的目的.
（1） 大小关系为
<
证明如下：
要证<，只需证
<
,
因为a、b、c>0, 只需证b2<ac,
因为
、
、
成等差数列，所以
=+
2
，
所以b2
ac 成立
又因为a、b、c任意两边均不相等，所以b2<ac 成立
故所得大小关系正确.
- 假设B是钝角，则cosB<0，而cosB=
>
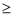
>0
这与cosB<0矛盾，故假设不成立，所以B不可能是钝角.
练习册系列答案
相关题目
【题目】某小学对一年级的甲、乙两个班进行“数学学前教育”对“小学数学成绩优秀”影响的试验，其中甲班为试验班(实施了数学学前教育)，乙班为对比班(和甲班一样进行常规教学，但没有实施数学学前教育)，在期末测试后得到如下数据：
优秀人数 | 非优秀人数 | 总计 | |
甲班 | 30 | 20 | 50 |
乙班 | 25 | 25 | 50 |
总计 | 55 | 45 | 100 |
能否在犯错误的概率不超过0.01的前提下，认为进行“数学学前教育”对“小学数学成绩优秀”有积极作用？
【题目】为了普及环保知识,增强环保意识,某大学从理工类专业的A班和文史类专业的B班各抽取20名同学参加环保知识测试.统计得到成绩与专业的列联表如下所示:
优秀 | 非优秀 | 总计 | |
A班 | 14 | 6 | 20 |
B班 | 7 | 13 | 20 |
总计 | 21 | 19 | 40 |
则下列说法正确的是 ( )
A. 有99%的把握认为环保知识测试成绩与专业有关
B. 有99%的把握认为环保知识测试成绩与专业无关
C. 有95%的把握认为环保知识测试成绩与专业有关
D. 有95%的把握认为环保知识测试成绩与专业无关