题目内容
为了解某班学生喜爱打篮球是否与性别有关,对本班50人进行了问卷调查得到了如下列表:
| | 喜爱打篮球 | 不喜爱打篮球 | 合计 |
| 男生 | | 5 | |
| 女生 | 10 | | |
| 合计 | | | 50 |
已知在全班50人中随机抽取1人,抽到喜爱打篮球的学生的概率为
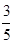 .
.(1)请将上表补充完整(不用写计算过程);
(2)能否有99.5%的把握认为喜爱打篮球与性别有关?说明你的理由.下面的临界值表供参考:
 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
(参考公式:
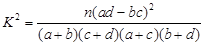 ,其中
,其中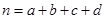 )
)
(1)见试题解析;(2)有99.5%的把握认为喜爱打篮球与性别有关
解析试题分析:(1)根据在全部50人中随机抽取1人抽到喜爱打篮球的学生的概率为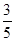 可得喜爱打篮球的学生,从而计算出喜欢打篮球的男生人数和不喜欢打篮球的人数,在计算出不会打篮球的女生数,即可得到列联表;(2)利用公式求得K2,与临界值比较,根据独立性检验的知识即可得到结论.
可得喜爱打篮球的学生,从而计算出喜欢打篮球的男生人数和不喜欢打篮球的人数,在计算出不会打篮球的女生数,即可得到列联表;(2)利用公式求得K2,与临界值比较,根据独立性检验的知识即可得到结论.
试题解析:(1) 已知在全班50人中随机抽取1人,抽到喜爱打篮球的学生的概率为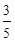
列联表如下: 喜爱打篮球 不喜爱打篮球 合计 男生 20 5 25 女生 10 15 25 合计 30 20 50
(2)∵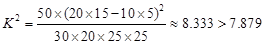
∴有99.5%的把握认为喜爱打篮球与性别有关. (14分)
考点:概率应用;2×2列联表;独立性检验

练习册系列答案
相关题目
计划在某水库建一座至多安装3台发电机的水电站,过去50年的水文资料显示,水库年入流量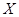 (年入流量:一年内上游来水与库区降水之和.单位:亿立方米)都在40以上.其中,不足80的年份有10年,不低于80且不超过120的年份有35年,超过120的年份有5年.将年入流量在以上三段的频率作为相应段的概率,并假设各年的年入流量相互独立.
(年入流量:一年内上游来水与库区降水之和.单位:亿立方米)都在40以上.其中,不足80的年份有10年,不低于80且不超过120的年份有35年,超过120的年份有5年.将年入流量在以上三段的频率作为相应段的概率,并假设各年的年入流量相互独立.
(1)求未来4年中,至多1年的年入流量超过120的概率;
(2)水电站希望安装的发电机尽可能运行,但每年发电机最多可运行台数受年入流量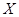 限制,并有如下关系:
限制,并有如下关系:
年入流量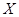 | 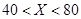 | 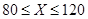 | 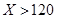 |
| 发电量最多可运行台数 | 1 | 2 | 3 |
若某台发电机运行,则该台年利润为5000万元;若某台发电机未运行,则该台年亏损800万元,欲使水电站年总利润的均值达到最大,应安装发电机多少台?
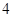 名男生和
名男生和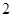 名女生中任选
名女生中任选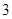 人参加演讲比赛,
人参加演讲比赛,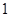 名女生的概率;
名女生的概率;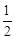 ,从陆路每个方向抵达灾区的概率都是
,从陆路每个方向抵达灾区的概率都是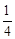 .
.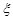 的数学期望.
的数学期望. 、
、 两项技术指标需要检测,设各项技术指标达标与否互不影响.若有且仅有一项技术指标达标的概率为
两项技术指标需要检测,设各项技术指标达标与否互不影响.若有且仅有一项技术指标达标的概率为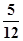 ,至少一项技术指标达标的概率为
,至少一项技术指标达标的概率为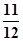 .按质量检验规定:两项技术指标都达标的零件为合格品.
.按质量检验规定:两项技术指标都达标的零件为合格品. 个,设
个,设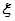 表示其中合格品的个数,求
表示其中合格品的个数,求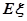 .
.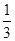 .
.