题目内容
【题目】设有关于x的一元二次方程![]() .
.
![]() 若a是从0,1,2三个数中任取的一个数,b是从0,1,2,3四个数中任取的一个数,求上述方程有实根的概率;
若a是从0,1,2三个数中任取的一个数,b是从0,1,2,3四个数中任取的一个数,求上述方程有实根的概率;
![]() 若a是从区间
若a是从区间![]() 任取的一个数,b是从区间
任取的一个数,b是从区间![]() 任取的一个数,求上述方程有实数的概率.
任取的一个数,求上述方程有实数的概率.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
首先分析一元二次方程有实根的条件,得到a≥b
(1)本题是一个古典概型,试验发生包含的基本事件可以通过列举得到结果数,满足条件的事件在前面列举的基础上得到结果数,求得概率.
(2)本题是一个几何概型,试验的全部结果所构成的区域为{(a,b)|0≤a≤2,0≤b≤3},满足条件的构成事件A的区域为{(a,b)|0≤a≤2,0≤b≤3,a≥b},根据概率等于面积之比,得到概率.
设事件A为“方程有实根”.
当a>0,b>0时,方程有实根的充要条件为a≥b
(1)由题意知本题是一个古典概型,试验发生包含的基本事件共12个:
(0,0)(0,1)(0,2)(0,3)(1,0)(1,1)(1,2)(1,3)(2,0)(2,1)(2,2)(2,3)
其中第一个数表示a的取值,第二个数表示b的取值.
事件A中包含6个基本事件,
∴事件A发生的概率为P![]() ;
;
(2)由题意知本题是一个几何概型,
试验的全部结果所构成的区域为{(a,b)|0≤a≤2,0≤b≤3}
满足条件的构成事件A的区域为{(a,b)|0≤a≤2,0≤b≤3,a≥b}
∴所求的概率是 .
.

【题目】铁人中学高二学年某学生对其亲属30人![]() 饮食习惯进行了一次调查,并用如图所示的茎叶图表示30人的饮食指数.(说明:图中饮食指数低于70的人,饮食以蔬菜为主;饮食指数高于70的人,饮食以肉类为主.)
饮食习惯进行了一次调查,并用如图所示的茎叶图表示30人的饮食指数.(说明:图中饮食指数低于70的人,饮食以蔬菜为主;饮食指数高于70的人,饮食以肉类为主.)
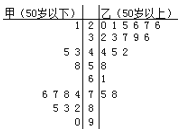
(Ⅰ)根据茎叶图,帮助这位学生说明其亲属30人的饮食习惯;
(Ⅱ)根据以上数据完成下列![]() 的列联表:
的列联表:
主食蔬菜 | 主食肉类 | 合计 | |
50岁以下人数 | |||
50岁以上人数 | |||
合计人数 |
(Ⅲ)能否在犯错误的概率不超过0.01的前提下认为其亲属的饮食习惯与年龄有关系?
附:![]() .
.
| 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |