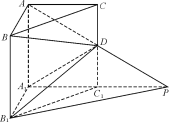
题目内容
【题目】某公司计划在迎春节联欢会中设一项抽奖活动:在一个不透明的口袋中装入外形一样号
码分别为1,2,3,…,10的十个小球。活动者一次从中摸出三个小球,三球号码有且仅有两个连号的为三等奖,奖金30元;三球号码都连号为二等奖,奖金60元;三球号码分别为1,5,10为一等奖,奖金240元;其余情况无奖金。
(1)求员工甲抽奖一次所得奖金ξ的分布列与期望;
(2)员工乙幸运地先后获得四次抽奖机会,他得奖次数![]() 的方差是多少?
的方差是多少?
【答案】
E |
E |
![]()

【解析】
试题分析:本题主要考查生活中的概率知识,离散型随机变量的分布列和数学期望以及二项分布的方差问题,考查学生的分析能力和计算能力.第一问,10个球中摸3个,所以基本事件总数为![]() ,
,![]() 的可能取值为4种,分别数出每一种情况符合题意的种数,与基本事件总数相除求出4个概率值,列出分布列,利用
的可能取值为4种,分别数出每一种情况符合题意的种数,与基本事件总数相除求出4个概率值,列出分布列,利用![]() 求期望;第二问,利用第一问分布列的结论,用间接法先求出乙一次抽奖中奖的概率,通过分析题意,可得中奖次数
求期望;第二问,利用第一问分布列的结论,用间接法先求出乙一次抽奖中奖的概率,通过分析题意,可得中奖次数![]() 符合二项分布,利用
符合二项分布,利用![]() 的公式计算方差.
的公式计算方差.
试题解析:(1)甲抽奖一次,基本事件的总数为![]() ,奖金
,奖金![]() 的所有可能取值为0,30,60,240.
的所有可能取值为0,30,60,240.
一等奖的情况只有一种,所有奖金为120元的概率为![]() ,
,
三球连号的情况有1,2,3;2,3,4;……8,9,10共8种,得60元的概率为![]() ,
,
仅有两球连号中,对应1,2与9,10的各有7种:对应2,3;3,4;……8,9各有6种.
得奖金30元的概率为![]() ,
,
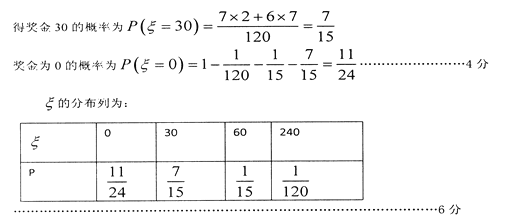
得奖金0元的概率为![]() , 4分
, 4分
![]() 的分布列为:
的分布列为:
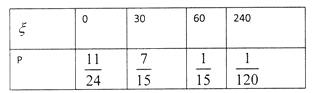 6分
6分
![]() 8分
8分
(2)由(1)可得乙一次抽奖中中奖的概率为![]()
四次抽奖是相互独立的,所以中奖次数![]()
故![]() . 12分
. 12分

【题目】高考复习经过二轮“见多识广”之后,为了研究考前“限时抢分”强化训练次数![]() 与答题正确率
与答题正确率![]() ﹪的关系,对某校高三某班学生进行了关注统计,得到如下数据:
﹪的关系,对某校高三某班学生进行了关注统计,得到如下数据:
| 1 | 2 | 3 | 4 |
| 20 | 30 | 50 | 60 |
(1)求![]() 关于
关于![]() 的线性回归方程,并预测答题正确率是100﹪的强化训练次数;
的线性回归方程,并预测答题正确率是100﹪的强化训练次数;
(2)若用![]() 表示统计数据的“强化均值”(精确到整数),若“强化均值”的标准差在区间
表示统计数据的“强化均值”(精确到整数),若“强化均值”的标准差在区间![]() 内,则强化训练有效,请问这个班的强化训练是否有效?
内,则强化训练有效,请问这个班的强化训练是否有效?
附:回归直线的斜率和截距的最小二乘法估计公式分别为:
 ,
,![]() =
=![]() -
-![]()
![]() ,
,
样本数据![]() 的标准差为:
的标准差为: .
.