题目内容
【题目】已知圆C经过点A(﹣2,0),B(0,2),且圆心C在直线y=x上,又直线l:y=kx+1与圆C相交于P、Q两点.
(1)求圆C的方程;
(2)若![]() ,求实数k的值;
,求实数k的值;
(3)过点(0,4)作动直线m交圆C于E,F两点.试问:在以EF为直径的所有圆中,是否存在这样的圆P,使得圆P经过点M(2,0)?若存在,求出圆P的方程;若不存在,请说明理由.
【答案】(1)x2+y2=4(2)k=0(3)存在圆P:5x2+5y2﹣16x﹣8y+12=0或x2+y2=4,使得圆P经过点M(2,0).
【解析】试题分析:(1)先求出AB中垂线方程,再与直线y=x联立求出交点即为圆心,最后根据圆心到A点距离等于半径,写出圆方程(2)联立直线y=kx+1与圆方程,根据向量数量积以及韦达定理化简可得实数k的值;(3)设E,F坐标,则可表示出以EF为直径的圆方程,再设直线m点斜式方程与圆C方程联立,利用韦达定理以及以EF为直径的圆过点M(2,0)求出直线m斜率,代入即得以EF为直径的圆方程,最后讨论直线m斜率不存在时是否满足题意
试题解析:解:(1)设圆心C(a,a),半径为r.
因为圆C经过点A(﹣2,0),B(0,2),
所以|AC|=|BC|=r,
即 ,
,
解得a=0,r=2,
所以圆C的方程是x2+y2=4.
(2)因为![]()
![]() =2×2×cos<
=2×2×cos<![]() ,
,![]() >=﹣2,
>=﹣2,
且![]() 与
与![]() 的夹角为∠POQ,
的夹角为∠POQ,
所以cos∠POQ=﹣![]() ,∠POQ=120°,
,∠POQ=120°,
所以圆心C到直线l:kx﹣y+1=0的距离d=1,
又d=![]() ,所以k=0.
,所以k=0.
(3)(ⅰ)当直线m的斜率不存在时,
直线m经过圆C的圆心C,
此时直线m与圆C的交点为E(0,2),F(0,﹣2),
EF即为圆C的直径,而点M(2,0)在圆C上,
即圆C也是满足题意的圆.
(ⅱ)当直线m的斜率存在时,设直线m:y=kx+4,
由![]() ,消去y整理,得(1+k2)x2+8kx+12=0,
,消去y整理,得(1+k2)x2+8kx+12=0,
由△=64k2﹣48(1+k2)>0,得![]() 或
或![]() .
.
设E(x1,y1),F(x2,y2),
则有 ①…
①…
由①得![]() ,②
,②![]() ,③
,③
若存在以EF为直径的圆P经过点M(2,0),则ME⊥MF,
所以![]() ,
,
因此(x1﹣2)(x2﹣2)+y1y2=0,
即x1x2﹣2(x1+x2)+4+y1y2=0,…
则![]() ,
,
所以16k+32=0,k=﹣2,满足题意.…
此时以EF为直径的圆的方程为x2+y2﹣(x1+x2)x﹣(y1+y2)y+x1x2+y1y2=0,
即![]() ,
,
亦即5x2+5y2﹣16x﹣8y+12=0.…
综上,在以EF为直径的所有圆中,
存在圆P:5x2+5y﹣16x﹣8y+12=0或x2+y2=4,使得圆P经过点M(2,0). …

 阅读快车系列答案
阅读快车系列答案【题目】某厂最近十年生产总量逐年上升,如表是部分统计数据:
年份 | 2008 | 2010 | 2012 | 2014 | 2016 |
生产总量(万吨) |
(Ⅰ)利用所给数据求年生产总量与年份之间的回归直线方程![]() ;
;
(Ⅱ)利用(Ⅰ)中所求出的直线方程预测该厂2018年生产总量.
(回归直线的方程: ![]() ,其中
,其中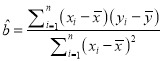 ,
, ![]() )
)