Question

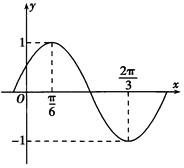
【题目】已知函f（x）=sin（ωx+φ）（ω＞0，|φ|＜π）的部分图象如图所示：

（1）求ω，φ的值；
（2）设g（x）=2 f（ ）f（ ）﹣1，当x∈[0， ]时，求函数g（x）的值域．

Answer 1

【答案】
（1）解：由图象知：T=4（ ）=π，则：ω= =2，

由f（0）=﹣1得：sinφ=﹣1，即：φ=kπ﹣ k∈Z，

∵|ω|＜π∴φ=﹣ ．

（2）解：由（1）知：f（x）=sin（2x﹣ ）=﹣cos2x，

∴g（x）=2 f（x）f（ ）﹣1=2 cosx[ ]﹣1

=cos2x+sin2x= sin（2x+ ），

当x∈[0， ]时，2x+ ∈ ，则sin（2x+ ）∈ ，

∴g（x）的值域为

【解析】（1）通过函数的图象求出函数周期，求出ω，利用f（0）=﹣1求出φ，得到函数的解析式．（2）利用（1）的结果求出g（x）的表达式，当x∈[0， ]时，求出2x+ ∈ ，然后求出函数的值域．
【考点精析】通过灵活运用三角函数的最值，掌握函数，当时，取得最小值为；当时，取得最大值为，则，，即可以解答此题．