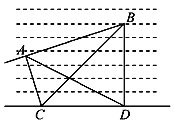
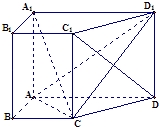
题目内容
【题目】如图,已知![]() 是棱长为3的正方体,点
是棱长为3的正方体,点![]() 在
在![]() 上,点
上,点![]() 在
在![]() 上,且
上,且![]() ,(1)求证:
,(1)求证: ![]() 四点共面; (2)若点
四点共面; (2)若点![]() 在
在![]() 上,
上, ![]() ,点
,点![]() 在
在![]() 上,
上, ![]() ,垂足为
,垂足为![]() ,求证:
,求证: ![]() 面
面![]() ; (3)用
; (3)用![]() 表示截面
表示截面![]() 和面
和面![]() 所成锐二面角大小,求
所成锐二面角大小,求![]() .
.

【答案】(1)证明见解析;(2)证明见解析;(3)![]()
【解析】试题分析:(1)四点共面问题通常我们将它们变成两条直线,然后证明这两条直线平行或相交,根据公理3的推论2、3可知,它们共面;(2)要证线面垂直,可以证明两个垂直平面内一条直线垂直两平面的交线即可;(3)可以证明![]() 就是二面角的平面角,在直角三角形中可解得
就是二面角的平面角,在直角三角形中可解得![]() 的值.
的值.
试题解析:(1)证明:在DD![]() 上取一点N使得DN=1,连接CN,EN,显然四边形CFD
上取一点N使得DN=1,连接CN,EN,显然四边形CFD![]() N是平行四边形,所以D
N是平行四边形,所以D![]() F//CN,同理四边形DNEA是平行四边形,所以EN//AD,且EN=AD,又BC//AD,且AD=BC,所以EN//BC,EN=BC,所以四边形CNEB是平行四边形,所以
F//CN,同理四边形DNEA是平行四边形,所以EN//AD,且EN=AD,又BC//AD,且AD=BC,所以EN//BC,EN=BC,所以四边形CNEB是平行四边形,所以
CN//BE,所以D![]() F//BE,所以
F//BE,所以![]() 四点共面。
四点共面。
(2)因为![]() 所以
所以![]() ∽
∽![]() MBG,所以
MBG,所以![]() ,即
,即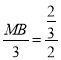 ,所以MB=1,因为AE=1,所以四边形ABME是矩形,所以EM⊥BB
,所以MB=1,因为AE=1,所以四边形ABME是矩形,所以EM⊥BB![]() 又平面ABB
又平面ABB![]() A
A![]() ⊥平面BCC
⊥平面BCC![]() B
B![]()
,且EM在平面ABB![]() A
A![]() 内,所以
内,所以![]() 面
面![]()
(3)![]() 面
面![]() ,所以
,所以![]() BF,
BF, ![]() MH,
MH, ![]() ,所以∠MHE就是截面
,所以∠MHE就是截面![]() 和面
和面![]() 所成锐二面角的平面角,∠EMH=
所成锐二面角的平面角,∠EMH=![]() ,所以
,所以![]() ,ME=AB=3,
,ME=AB=3, ![]() ∽
∽![]() MHB,所以3:MH=BF:1,BF=
MHB,所以3:MH=BF:1,BF=![]() ,所以MH=
,所以MH=![]() ,所以
,所以![]() =
=![]()

练习册系列答案
相关题目