题目内容
在一次联考后,某校对甲、乙两个文科班的数学考试成绩进行分析,规定:大于或等于 分为优秀,
分为优秀, 分以下为非优秀,统计成绩后,得到如下的
分以下为非优秀,统计成绩后,得到如下的 列联表,且已知在甲、乙两个文科班全部
列联表,且已知在甲、乙两个文科班全部 人中随机抽取人为优秀的概率为
人中随机抽取人为优秀的概率为 .
.
| | 优秀 | 非优秀 | 合计 |
| 甲班 |  | | |
| 乙班 | |  | |
| 合计 | | |  |
(2)根据列联表的数据,能否有
 的把握认为成绩与班级有关系?
的把握认为成绩与班级有关系?(3)在甲、乙两个理科班优秀的学生中随机抽取两名学生,用
 表示抽得甲班的学生人数,求
表示抽得甲班的学生人数,求 的分布列.
的分布列.
(1)详见解析;(2)按 的可靠性要求,能认为“成绩与班级有关系”;
的可靠性要求,能认为“成绩与班级有关系”;
(3)抽到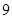 或
或 号的概率为
号的概率为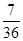 .
.
解析试题分析:(1)先根据题中条件确定乙班优秀的人数,然后根据甲乙两班的总人数将表中其它的数据补充上;(2)先提出假设“成绩与班级无关”,根据表中数据求出 某食品企业一个月内被消费者投诉的次数用 某品牌的汽车4S店,对最近100位采用分期付款的购车者进行统计,统计结果如下表所示: 某种产品按质量标准分为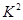 的值,然后利用临界值表确定犯错误的概率,进而确定是否有
的值,然后利用临界值表确定犯错误的概率,进而确定是否有 的把握认为成绩与班级有关系;(3)先确定随机变量
的把握认为成绩与班级有关系;(3)先确定随机变量 的可能取值,然后根据超几何分布的方法求出随机变量
的可能取值,然后根据超几何分布的方法求出随机变量 在相应的取值下的概率,并列出相应的分布列.
在相应的取值下的概率,并列出相应的分布列.
试题解析:(1)列联表如下表所示:
(2)假设成绩与班级无关,根据列联表中的数据,得到 优秀 非优秀 合计 甲班 
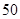
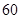
乙班 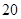

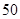
合计 
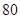

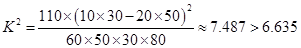 ,
,
因此按 的可靠性要求,能认为“成绩与班级有关系”;
的可靠性要求,能认为“成绩与班级有关系”;
(3)由(1)知,甲、乙两个理科班优秀的学生人数分别为 、
、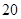 ,
,
依题意得, 的可能取值为
的可能取值为 、
、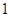 、
、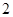 ,
, ,
, ,
,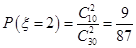 ,
,
所以 的分布列为:
的分布列为:


中考模拟卷江苏凤凰教育出版社系列答案
中考模拟试题汇编系列答案
中考内参系列答案

全程金卷冲刺100分系列答案
快乐2加1同步练习系列答案

名校名师培优全程检测卷系列答案
名师题库系列答案
本土教辅名校学案黄冈期末全程特训卷系列答案
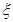 表示,椐统计,随机变量
表示,椐统计,随机变量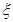 的概率分布如下:
的概率分布如下:
(1)求a的值和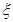
0
1
2
3
p
0.1
0.3
2a
a
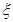 的数学期望;
的数学期望;
(2)假设一月份与二月份被消费者投诉的次数互不影响,求该企业在这两个月内共被消费者投诉2次的概率.
已知分3期付款的频率为0.2,4S店经销一辆该品牌的汽车,顾客分1期付款,其利润为1万元;分2期或3期付款,其利润为1.5万元;分4期或5期付款,其利润为2万元.用付款方式 分1期 分2期 分3期 分4期 分5期 频数 40 20 
10 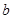
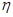 表示经销一辆汽车的利润.
表示经销一辆汽车的利润.
(1)求上表中 的值;
的值;
(2)若以频率作为概率,求事件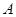 :“购买该品牌汽车的3位顾客中,至多有1位采用3期付款”的概率
:“购买该品牌汽车的3位顾客中,至多有1位采用3期付款”的概率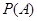 ;(3)求
;(3)求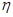 的分布列及数学期望
的分布列及数学期望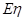 .
.  ,
, ,
,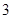 ,
,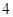 ,
,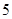 五个等级.现从一批该产品随机抽取20个,对其等级进行统计分析,得到频率分布表如下:
五个等级.现从一批该产品随机抽取20个,对其等级进行统计分析,得到频率分布表如下:
(1)在抽取的20个产品中,等级为5的恰有2个,求等级 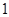
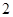
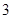
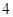
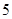
频率 
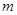
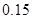

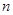
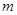 ,
,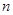 ;
;
(2)在(1)的条件下,从等级为3和5的所有产品中,任意抽取2个,求抽取的2个产品等级恰好相同的概率.
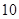 名同学,现测得排球队
名同学,现测得排球队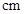 )分别是:
)分别是: 、
、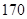 、
、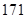 、
、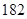 、
、 、
、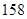 、
、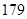 、
、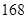 、
、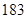 、
、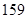 、
、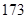 、
、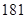 、
、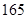 、
、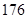 、
、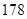 、
、
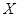 ,求
,求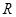 的函数:
的函数: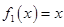 ,
,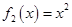 ,
,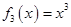 ,
, ,
,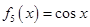 ,
,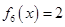 .
.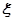 的分布列和数学期望.
的分布列和数学期望.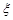 表示游客在甲、乙、丙三处旅游景点中选择游玩的景点数和没有选择游玩的景点数的乘积.
表示游客在甲、乙、丙三处旅游景点中选择游玩的景点数和没有选择游玩的景点数的乘积.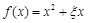 是R上的偶函数”为事件A,求事件A的概率;
是R上的偶函数”为事件A,求事件A的概率;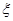 的概率分布列及数学期望.
的概率分布列及数学期望.

