题目内容
在一个盒子里装有4枝圆珠笔,其中3枝一等品,1枝三等品
(1)从盒子里任取2枝恰有1枝三等品的概率多大?
(2)从盒子里第一次任取1枝(不放回),第二次任取1枝;第一次取的是三等品,第二次取的是一等品的概率有多大?
(1)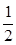 ;(2)
;(2)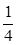
解析试题分析:(1)列举出“从盒子里任取2枝”所对应的的所有的可能的情况一共6种,在这6中里面找到符合“恰有1枝是三等品”的情况一共3种,用“恰有1枝是三等品”的情况数÷总的情况数即是所求的概率;(2)这是条件概率,可由条件概率的方法来作答,也可利用列举的方法,先列举出所有的“第一次任取1枝(不放回),第二次任取1枝”的情况数,然后在这些情况中找到符合“第一次取的是三等品,第二次取的是一等品”的情况数,用后者÷前者即是所求的概率
试题解析:(1)设三枝一等品为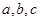 ,一枝三等品为
,一枝三等品为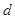 , 1分
, 1分
则“任取2枝”共有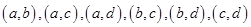 ,一共
,一共 种 4分
种 4分
“恰有一枝三等品”共有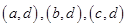 ,一共
,一共 种 5分
种 5分
所以“从盒子里任取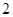 枝恰有
枝恰有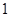 枝三等品”的概率是
枝三等品”的概率是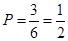 6分
6分
(2)“从盒子里第一次任取1枝(不放回),第二次任取1枝”,有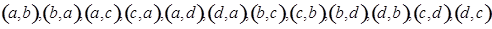 ,一共12种, 10分
,一共12种, 10分
其中“第一次取的是三等品,第二次取的是一等品”有 ,一共3种, 11分
,一共3种, 11分
所以“第一次取的是三等品,第二次取的是一等品”的概率是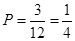 12分
12分
考点:1离散型随机变量及其应用;2随机事件的概率;3条件概率及其应用

 中考解读考点精练系列答案
中考解读考点精练系列答案学校为了使运动员顺利参加运动会,招募了8名男志愿者和12名女志愿者,这20名志愿者的身高如下茎叶图(单位:cm):若身高在180cm以上(包括180cm)定义为“高个子”,身高在180cm以下(不包括180cm)定义为“非高个子”,且只有“女高个子”才能担任“礼仪小姐”.
| 男 | | 女 | ||||||
| | | 8 | 16 | 5 | 8 | 9 | | |
| 8 | 7 | 6 | 17 | 2 | 3 | 5 | 5 | 6 |
| 7 | 4 | 2 | 18 | 0 | 1 | 2 | | |
| | | 1 | 19 | 0 | | | | |
(Ⅱ)若从所有“高个子”中随机选3名志愿者,用
 表示所选志愿者中能担任“礼仪小姐”的人数,试写出
表示所选志愿者中能担任“礼仪小姐”的人数,试写出 的分布列,并求
的分布列,并求 的数学期望.
的数学期望. 在一次联考后,某校对甲、乙两个文科班的数学考试成绩进行分析,规定:大于或等于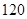 分为优秀,
分为优秀,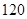 分以下为非优秀,统计成绩后,得到如下的
分以下为非优秀,统计成绩后,得到如下的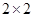 列联表,且已知在甲、乙两个文科班全部
列联表,且已知在甲、乙两个文科班全部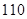 人中随机抽取人为优秀的概率为
人中随机抽取人为优秀的概率为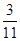 .
.
| | 优秀 | 非优秀 | 合计 |
| 甲班 | 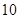 | | |
| 乙班 | | 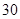 | |
| 合计 | | | 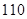 |
(2)根据列联表的数据,能否有
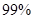 的把握认为成绩与班级有关系?
的把握认为成绩与班级有关系?(3)在甲、乙两个理科班优秀的学生中随机抽取两名学生,用
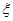 表示抽得甲班的学生人数,求
表示抽得甲班的学生人数,求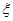 的分布列.
的分布列. 某超市为了解顾客的购物量及结算时间等信息,安排一名员工随机收集了在该超市购物的50位顾客的相关数据,如下表所示:
一次购物量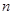 (件) (件) | 1≤n≤3 | 4≤n≤6 | 7≤n≤9 | 10≤n≤12 | n≥13 |
| 顾客数(人) |  | 20 | 10 | 5 | 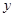 |
| 结算时间(分钟/人) | 0.5 | 1 | 1.5 | 2 | 2.5 |
(1)确定
 与
与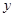 的值;
的值;(2)若将频率视为概率,求顾客一次购物的结算时间
 的分布列与数学期望;
的分布列与数学期望;(3)在(2)的条件下,若某顾客到达收银台时前面恰有2位顾客需结算,且各顾客的结算相互独立,求该顾客结算前的等候时间不超过2分钟的概率.
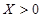 就去打球;若
就去打球;若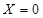 就去唱歌;若
就去唱歌;若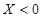 就去下棋.
就去下棋.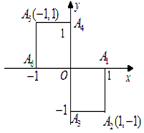
 个大小相同的小球,分别印有“多彩十艺节”和“美丽泉城行”两种标志,摇匀后,参加者每次从盒中同时抽取两个小球,若抽到两个球都印有“多彩十艺节”标志即可获奖.
个大小相同的小球,分别印有“多彩十艺节”和“美丽泉城行”两种标志,摇匀后,参加者每次从盒中同时抽取两个小球,若抽到两个球都印有“多彩十艺节”标志即可获奖. ,求抽奖者获奖的概率;
,求抽奖者获奖的概率;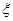 表示获奖的人数,求
表示获奖的人数,求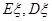 .
.