题目内容
一个盒子装有六张卡片,上面分别写着如下六个定义域为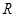 的函数:
的函数: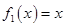 ,
, ,
,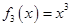 ,
,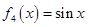 ,
,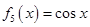 ,
,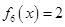 .
.
(1)现从盒子中任取两张卡片,将卡片上的函数相加得一个新函数,求所得函数是奇函数的概率;
(2)现从盒子中进行逐一抽取卡片,且每次取出后均不放回,若取到一张记有偶函数的卡片则停止抽取,否则继续进行,求抽取次数 的分布列和数学期望.
的分布列和数学期望.
(1)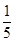 ;(2)详见解析.
;(2)详见解析.
解析试题分析:(1)利用性质“奇函数+奇函数=奇函数”这一性质得到所抽取的两个函数都是奇函数,然后再用排列组合结合古典概型的概率公式计算相应事件的概率;(2)先列举出随机变量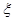 的全部可能取值,利用条件概率的计算公式计算随机变量子在相应的取值下对应的概率,从而列举出随机变量的分布列,最终计算出随机变量的数学期望.
的全部可能取值,利用条件概率的计算公式计算随机变量子在相应的取值下对应的概率,从而列举出随机变量的分布列,最终计算出随机变量的数学期望.
试题解析:(1)六个函数中是奇函数的有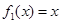 ,
,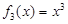 ,
,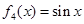 ,
,
由这3个奇函数中的任意两个函数相加均可得一个新的奇函数.
记事件A为“任取两张卡片,将卡片上的函数相加得到的函数是奇函数”,
由题意知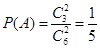 ;
;
(2) 可取1,2,3,4 ,
可取1,2,3,4 ,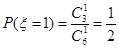 ,
, 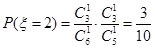
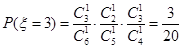 ,
, 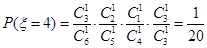 ,
,
故 的分布列为
的分布列为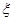
1 2 3 4 
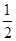
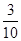
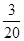
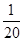
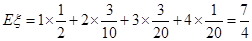
答: 的数学期望为
的数学期望为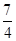 .
.
考点:1.排列组合;2.条件概率;3.随机变量的概率分布列与数学期望

练习册系列答案
 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案
相关题目
为了解某班学生喜爱打篮球是否与性别有关,对本班50人进行了问卷调查得到了如下列表:
| | 喜爱打篮球 | 不喜爱打篮球 | 合计 |
| 男生 | | 5 | |
| 女生 | 10 | | |
| 合计 | | | 50 |
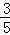 .
.(1)请将上面的列联表补充完整(不用写计算过程);
(2)能否在犯错误的概率不超过0.005的前提下认为喜爱打篮球与性别有关?说明你的理由;
(3)现从女生中抽取2人进一步调查,设其中喜爱打篮球的女生人数为ξ,求ξ的分布列与期望.
下面的临界值表供参考:
| P(K2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
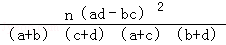 ,其中n=a+b+c+d)
,其中n=a+b+c+d) 在一次联考后,某校对甲、乙两个文科班的数学考试成绩进行分析,规定:大于或等于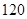 分为优秀,
分为优秀,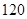 分以下为非优秀,统计成绩后,得到如下的
分以下为非优秀,统计成绩后,得到如下的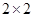 列联表,且已知在甲、乙两个文科班全部
列联表,且已知在甲、乙两个文科班全部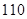 人中随机抽取人为优秀的概率为
人中随机抽取人为优秀的概率为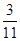 .
.
| | 优秀 | 非优秀 | 合计 |
| 甲班 | 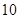 | | |
| 乙班 | | 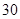 | |
| 合计 | | |  |
(2)根据列联表的数据,能否有
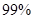 的把握认为成绩与班级有关系?
的把握认为成绩与班级有关系?(3)在甲、乙两个理科班优秀的学生中随机抽取两名学生,用
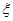 表示抽得甲班的学生人数,求
表示抽得甲班的学生人数,求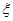 的分布列.
的分布列.  小时抽一包产品,称其重量(单位:克)是否合格,分别记录抽查数据,获得重量数据的茎叶图如图所示.
小时抽一包产品,称其重量(单位:克)是否合格,分别记录抽查数据,获得重量数据的茎叶图如图所示.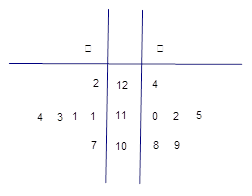
 件样品中随机抽取两件,求所抽取的两件样品的重量之差不超过
件样品中随机抽取两件,求所抽取的两件样品的重量之差不超过 克的概率.
克的概率.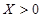 就去打球;若
就去打球;若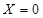 就去唱歌;若
就去唱歌;若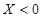 就去下棋.
就去下棋.
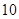 个大小相同的小球,分别印有“多彩十艺节”和“美丽泉城行”两种标志,摇匀后,参加者每次从盒中同时抽取两个小球,若抽到两个球都印有“多彩十艺节”标志即可获奖.
个大小相同的小球,分别印有“多彩十艺节”和“美丽泉城行”两种标志,摇匀后,参加者每次从盒中同时抽取两个小球,若抽到两个球都印有“多彩十艺节”标志即可获奖. ,求抽奖者获奖的概率;
,求抽奖者获奖的概率;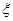 表示获奖的人数,求
表示获奖的人数,求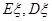 .
.

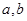 的值及分数在
的值及分数在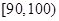 范围内的学生数,并估计这次考试全校学生数学成绩及格率(分数在
范围内的学生数,并估计这次考试全校学生数学成绩及格率(分数在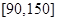 范围为及格);
范围为及格);