题目内容
某品牌的汽车4S店,对最近100位采用分期付款的购车者进行统计,统计结果如下表所示:
| 付款方式 | 分1期 | 分2期 | 分3期 | 分4期 | 分5期 |
| 频数 | 40 | 20 | 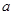 | 10 | 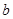 |
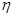 表示经销一辆汽车的利润.
表示经销一辆汽车的利润.(1)求上表中
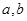 的值;
的值;(2)若以频率作为概率,求事件
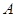 :“购买该品牌汽车的3位顾客中,至多有1位采用3期付款”的概率
:“购买该品牌汽车的3位顾客中,至多有1位采用3期付款”的概率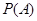 ;(3)求
;(3)求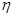 的分布列及数学期望
的分布列及数学期望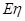 .
.
(1) 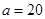 ,
,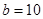 ;(2)0.896;(3)分布列见解析,
;(2)0.896;(3)分布列见解析,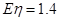 .
.
解析试题分析:(1)由条件“分3期付款的频率为0.2”与“100位”即可分别求出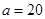 和
和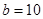 ;(2)由题意可知分3期付款的概率为0.2,事件
;(2)由题意可知分3期付款的概率为0.2,事件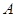 :“购买该品牌汽车的3位顾客中,至多有1位采用3期付款”即分为全部未采用3期付款和只有1位采用3期付款这两种情况,即得
:“购买该品牌汽车的3位顾客中,至多有1位采用3期付款”即分为全部未采用3期付款和只有1位采用3期付款这两种情况,即得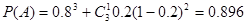 ;(3)先将
;(3)先将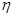 所有可能取值所对应的相应概率计算出来,然后即可列出分布列,再由期望的定义根据分布列的情况即可得出本题的解.
所有可能取值所对应的相应概率计算出来,然后即可列出分布列,再由期望的定义根据分布列的情况即可得出本题的解.
试题解析:(1)由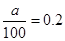 得
得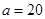 ,因为
,因为 ,所以
,所以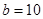 , 2分
, 2分
(2)“购买该品牌汽车的3位顾客中至多有1位采用3期付款”的概率: 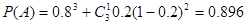 6分
6分
(3)记分期付款的期数为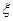 ,依题意得
,依题意得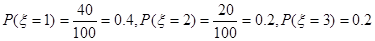
 10分
10分
因为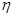 的可能取值为1,1.5,2(单位万元),并且
的可能取值为1,1.5,2(单位万元),并且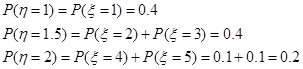
所以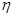 的分布列为
的分布列为
所以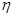
1 1.5 2 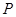
0.4 0.4 0.2 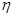 的数学期望为
的数学期望为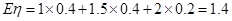 (万元) 12分
(万元) 12分
考点:1.频率;2.随机事件的概率;3.分布列与期望.

 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案为了参加2013年市级高中篮球比赛,该市的某区决定从四所高中学校选出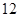 人组成男子篮球队代表所在区参赛,队员来源人数如下表:
人组成男子篮球队代表所在区参赛,队员来源人数如下表:
| 学校 | 学校甲 | 学校乙 | 学校丙 | 学校丁 |
| 人数 | 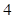 | 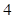 | 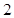 | 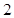 |
(Ⅰ)求这两名队员来自同一学校的概率;
(Ⅱ)设选出的两名队员中来自学校甲的人数为
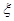 ,求随机变量
,求随机变量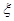 的分布列及数学期望
的分布列及数学期望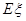 .
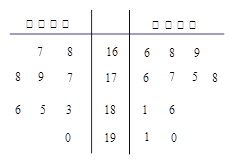
. 学校为了使运动员顺利参加运动会,招募了8名男志愿者和12名女志愿者,这20名志愿者的身高如下茎叶图(单位:cm):若身高在180cm以上(包括180cm)定义为“高个子”,身高在180cm以下(不包括180cm)定义为“非高个子”,且只有“女高个子”才能担任“礼仪小姐”.
| 男 | | 女 | ||||||
| | | 8 | 16 | 5 | 8 | 9 | | |
| 8 | 7 | 6 | 17 | 2 | 3 | 5 | 5 | 6 |
| 7 | 4 | 2 | 18 | 0 | 1 | 2 | | |
| | | 1 | 19 | 0 | | | | |
(Ⅱ)若从所有“高个子”中随机选3名志愿者,用
 表示所选志愿者中能担任“礼仪小姐”的人数,试写出
表示所选志愿者中能担任“礼仪小姐”的人数,试写出 的分布列,并求
的分布列,并求 的数学期望.
的数学期望. 在一次联考后,某校对甲、乙两个文科班的数学考试成绩进行分析,规定:大于或等于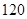 分为优秀,
分为优秀,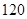 分以下为非优秀,统计成绩后,得到如下的
分以下为非优秀,统计成绩后,得到如下的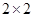 列联表,且已知在甲、乙两个文科班全部
列联表,且已知在甲、乙两个文科班全部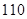 人中随机抽取人为优秀的概率为
人中随机抽取人为优秀的概率为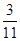 .
.
| | 优秀 | 非优秀 | 合计 |
| 甲班 | 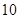 | | |
| 乙班 | | 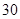 | |
| 合计 | | |  |
(2)根据列联表的数据,能否有
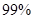 的把握认为成绩与班级有关系?
的把握认为成绩与班级有关系?(3)在甲、乙两个理科班优秀的学生中随机抽取两名学生,用
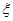 表示抽得甲班的学生人数,求
表示抽得甲班的学生人数,求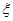 的分布列.
的分布列. 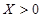 就去打球;若
就去打球;若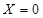 就去唱歌;若
就去唱歌;若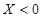 就去下棋.
就去下棋.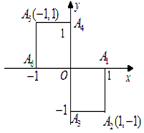
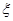 ,求
,求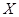 为选取女生的人数,求
为选取女生的人数,求