题目内容
已知直线l1,l2方程分别为2x-y=0,x-2y+3=0,且l1,l2的交点为P.
(1)求P点坐标;
(2)若直线l过点P,且到坐标原点的距离为1,求直线l的方程.
(1)求P点坐标;
(2)若直线l过点P,且到坐标原点的距离为1,求直线l的方程.
(1)联立直线l1,l2方程可得
,解得P(1,2).
(2)①当过点P(1,2)的直线与x轴垂直时,则点A(1,2)到原点的距离为1,∴x=1为所求直线方程.
②当过点A(1,2)且与x轴不垂直时,可设所求直线方程为y-2=k(x-1),
即:kx-y-k+2=0,由点P到坐标原点的距离为1得到
=1,解得k=
,
故所求的直线方程为y-2=
(x-1),即3x-4y+5=0.
综上:所求直线方程为x=1或3x-4y+5=0.
|
(2)①当过点P(1,2)的直线与x轴垂直时,则点A(1,2)到原点的距离为1,∴x=1为所求直线方程.
②当过点A(1,2)且与x轴不垂直时,可设所求直线方程为y-2=k(x-1),
即:kx-y-k+2=0,由点P到坐标原点的距离为1得到
| |-k+2| | ||
|
| 3 |
| 4 |
故所求的直线方程为y-2=
| 3 |
| 4 |
综上:所求直线方程为x=1或3x-4y+5=0.

练习册系列答案
相关题目
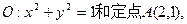 由⊙O外一点P(a,b)向⊙O引切线PQ,切点为Q,且满足
由⊙O外一点P(a,b)向⊙O引切线PQ,切点为Q,且满足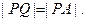 (1)求实数a,b间满足的等量关系;(2)求线段PQ长的最小值;
(1)求实数a,b间满足的等量关系;(2)求线段PQ长的最小值;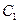 :
: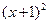 +
+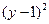 =1,圆
=1,圆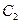 与圆
与圆 于直线
于直线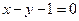 对称,则圆
对称,则圆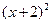 +
+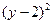 ="1 " b.
="1 " b.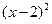 +
+ =1
=1