题目内容
若圆C:x2+y2-4x-4y-10=0上至少有三个不同的点到直线l:x-y+c=0的距离为2
,则c的取值范围是( )
| 2 |
A.[-2
| B.(-2
| C.[-2,2] | D.(-2,2) |
圆x2+y2-4x-4y-10=0整理为(x-2)2+(y-2)2=18,
∴圆心坐标为(2,2),半径为3
,
要求圆上至少有三个不同的点到直线l:x-y+c=0的距离为2
则圆心到直线的距离d≤
≤
,
∴-2≤c≤2
故选C
∴圆心坐标为(2,2),半径为3
| 2 |
要求圆上至少有三个不同的点到直线l:x-y+c=0的距离为2
| 2 |
则圆心到直线的距离d≤
| 2 |
| |c| | ||
|
| 2 |
∴-2≤c≤2
故选C

练习册系列答案
相关题目
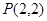 ,圆
,圆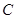 :
: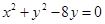 ,过点
,过点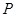 的动直线
的动直线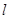 与圆
与圆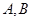 两点,线段
两点,线段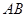 的中点为
的中点为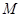 ,
,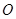 为坐标原点.
为坐标原点.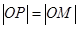 时,求
时,求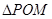 的面积
的面积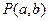
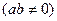 是圆
是圆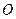 :
: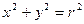 内一点,直线
内一点,直线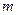 是以
是以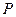 为中点的弦所在的直线,若直线
为中点的弦所在的直线,若直线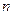 的方程为
的方程为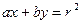 ,则
,则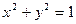 上的点到直线
上的点到直线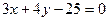 的距离的最小值是( )
的距离的最小值是( )